Clasificar las cónicas a partir del análisis del discriminante
1) Si A y C tienen el mismo signo y el valor de B es cero, la diferencia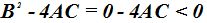 
será negativa.
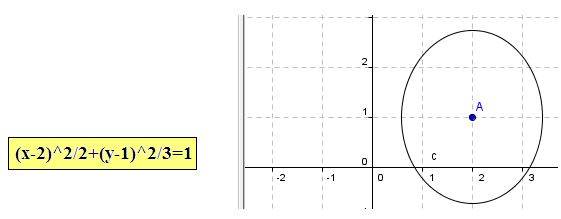
Cuando A y C son positivos iguales y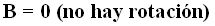 
se trata de una elipse:
2) Si A y C tienen distinto signo y B = 0, el discriminante tendrá signo positivo:
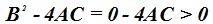
Ejemplo:
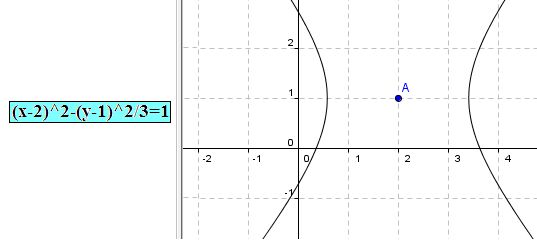
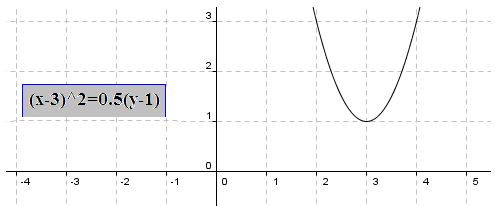
3) En el caso de que el discriminante vale cero, es decir, que el coeficiente de A sea positivo y los coeficientes B y C sean iguales a cero nos referimos a una parábola
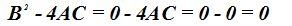
Ejemplo:
En resumen:
