Volúmenes de un Prisma - Paralelepípedos - Pirámides Rectas y Oblícuas - Altura de una Pirámide
El volumen de un prisma recto cualquiera se calcula multiplicando el:
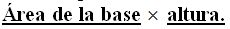
15(3).24 Un prisma triangular tiene por base un triángulo equilátero de 2 metros de lado.
La altura del prisma mide 3 metros. ¿Cuántos litros de agua puede contener?
Respuesta: 5.190 litros.
Solución
La base es un triángulo equilátero de lado 2.
Desconocemos la altura.
Podemos dibujar el triángulo equilátero incluyendo los datos conocidos:
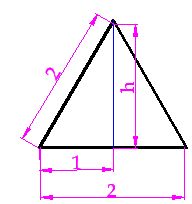
La altura del triángulo la hemos representado por h.
La altura divide al lado opuesto en dos partes iguales. Esto quiere decir que, cada mitad del lado vale 1 metro.
Si giramos el triángulo con sus datos hacia la derecha 90º obtendríamos:
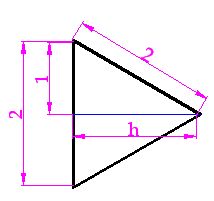
Teniendo en cuenta que lo que tenemos que calcular es el valor de h, observarás que es un cateto del triángulo rectángulo:
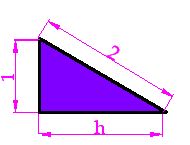
Haciendo uso del teorema de Pitágoras tenemos:
Hipotenusa al cuadrado es igual a la suma de los cuadrados de los catetos:
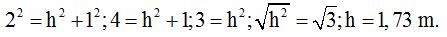
Ahora podemos calcular el área de la base:
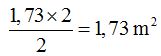
El volumen del prisma será: 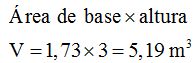
Como sabemos que en 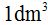 cabe 1 litro de agua, pasamos:
cabe 1 litro de agua, pasamos: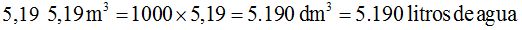
15(3).25 En una piscina de forma cuadrada de 10 m. de lado caben 300.000 litros de agua. ¿Cuál es su profundidad?
Respuesta: 3 m. de altura
Solución
El volumen equivale a 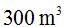 por lo que podemos escribir la siguiente ecuación:
por lo que podemos escribir la siguiente ecuación: 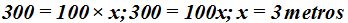
PARALELEPÍPEDOS.
La palabra paralelepípedo, bastante larga por cierto, procede del griego: paralelos y epipedon que significa plano, superficie,…
Luego, la palabra paralelepípedo significa de planos o superficies paralelos.
Todos los prismas cuyas bases sean paralelogramos llamamos paralelepípedos.
Recuerda que un paralelogramo es un polígono de cuatro lados y éstos son paralelos dos a dos.
Ejemplo:
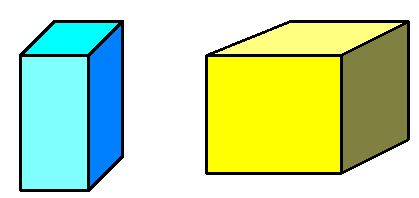
El volumen, dado que son prismas, será: 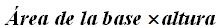
PIRÁMIDE
La pirámide es un poliedro que tiene por base un polígono y sus caras laterales son triángulos que se juntan en un punto llamado vértice de la pirámide.
Esta palabra procede del griego piros que significa fuego, quizá por la forma de la llama.
PIRÁMIDES RECTAS Y OBLICUAS:
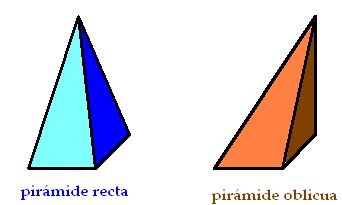
Las pirámides se dividen en dos grupos, como los poliedros:
Pirámides rectas o regulares y las oblicuas.
Una pirámide es recta o regular cuando todas las caras laterales son triángulos isósceles iguales. Cuando sus caras laterales no son triángulos equiláteros iguales, se trata de pirámides oblicuas.
Según el número de lados del polígono de la base, las pirámides se llaman triangulares, cuadrangulares, pentagonales, etc.
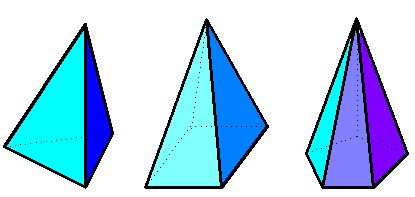
Construcción de una pirámide cuadrangular:
Sobre una cartulina dibujas una plantilla que se parezca a:
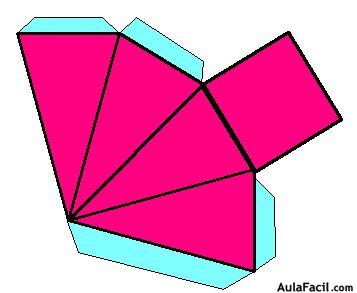
Doblas la cartulina por las líneas, aplicas pegamento en las solapas y las pegas.
Construcción de una pirámide hexagonal:
Del mismo que en el caso anterior, con la siguiente plantilla:
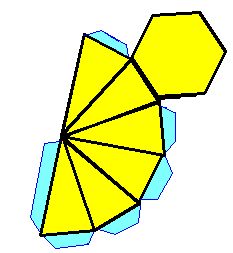
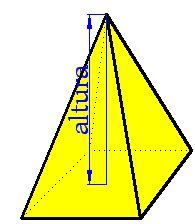
ALTURA DE UNA PIRÁMIDE.
La altura de una pirámide es la distancia entre el vértice de la pirámide y la base de la misma: