Rectángulo Aúreo
Se llama rectángulo áureo al que el cociente entre el valor del lado mayor entre el menor nos da el número de oro o cociente áureo.
En este momento posiblemente digas, con toda razón: “no me he enterado de nada”.
Después de hacer los doce pasos siguientes te habrás enterado de la mitad.
Vas a hacer lo siguiente:
1) Toma un papel, un bolígrafo, una regla y un compás.
2) Dibuja un cuadrado que tenga 2 cm. de lado:
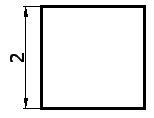
3) Halla el punto medio de la base (en la figura, el punto rojo):
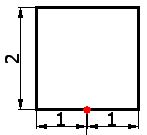
Cada mitad de la base vale 1 cm.
4) Toma la regla y une el punto medio anterior con el vértice superior derecho
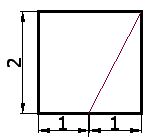
5) Toma el compás y haciendo centro en el punto medio de la base (punto rojo figura del apartado 3) y con radio igual a la longitud de la recta que acabas de trazar dibuja una circunferencia:
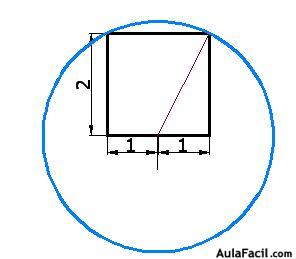
6) Prolonga la línea de la base hasta cortarse con la circunferencia y borra parte de la circunferencia para que te quede:
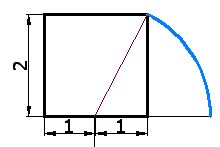
7) Calculamos la longitud del radio de la circunferencia, es decir, de r:
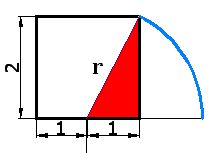
El triángulo de color rojo es un triángulo rectángulo en el que los catetos valen 1 cm. y 2 cm. siendo r el valor de la hipotenusa.
Haciendo uso del teorema de Pitágoras escribimos:
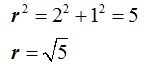
8) La línea de color amarillo de la siguiente figura valdrá:
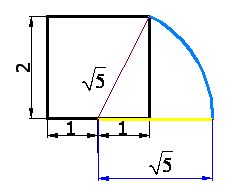
Por tratarse del radio (hipotenusa del dibujo anterior).
9) ¿Cuánto vale la línea ![]() de figura siguiente?
de figura siguiente?
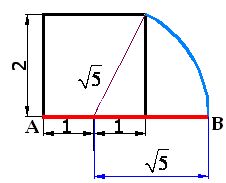
La línea de color rojo mide 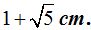
10) Traza una perpendicular de 2 cm. a la línea 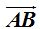 en el punto B:
en el punto B:
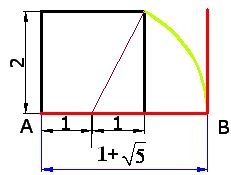
La base completa en color rojo ahora mide 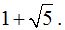
11) Unimos el vértice superior derecho del cuadrado con la perpendicular al punto B, de la base y escribes las medidas del nuevo rectángulo:
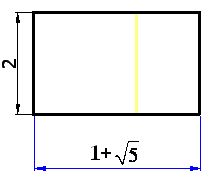
12) Recuerda que llamamos razón al cociente indicado de dos números.
Si divides el valor del lado mayor 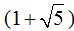 entre el valor del lado menor (2), es decir:
entre el valor del lado menor (2), es decir:
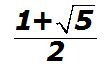
a este cociente indicado o razón llamamos razón áurea, y el valor que se obtienes de este cociente llamamos número de oro o número áureo que se representa por la letra griega 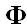 (se lee FI) y vale:
(se lee FI) y vale:
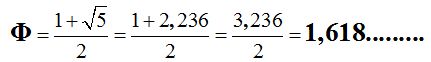
Dirás que hasta has entendido, pero todo esto ¿para qué? ¿para qué sirve saber esto?
Los griegos, varios siglos antes de Cristo decían que este rectángulo era armonioso que tenía una extraordinaria belleza, de tal modo que utilizaban estas proporciones a sus más famosos monumentos (Partenón, si encuentras una fotografía toma las medidas de su anchura y altura y te encontrarás con el número de oro).
También los egipcios hicieron uso de la razón áurea (pirámide de Keops).
Varios siglos después, uno de las mentes más grandes que han existido en la humanidad, Leonardo da Vinci que vivió entre los años 1452 y 1519 profundizó en los estudios y aplicaciones (cuerpo humano-perfección de su anatomía, Mona Lisa, etc.) de  y fue él quien dio los nombres de razón áurea, número de oro, etc.
y fue él quien dio los nombres de razón áurea, número de oro, etc.
Ejercicio:
Tu tarjeta del D.N.I ¿tiene forma de un rectángulo de oro o rectángulo áureo?.Comprueba.
Para los griegos el rectángulo áureo era un rectángulo además de bello por sus proporciones, era misterioso. Existen muchos trabajos, estudios sobre algunas figuras geométricas basadas en este rectángulo, que si te gusta investigar encontrarás cosas muy interesantes. Merece la pena.
Espiral áurea:
Disponemos de un rectángulo áureo tal como lo tienes en la figura siguiente:
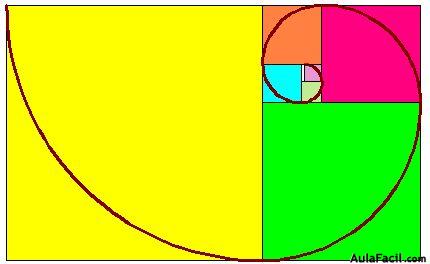
Determinamos el cuadrado mayor (amarillo) y trazamos un arco de circunferencia con centro en el vértice superior derecho e inicio en el ángulo superior izquierdo y final del arco en el vértice inferior derecho de dicho cuadrado.
El resto de la figura, es decir, todo el dibujo que nos queda prescindiendo del cuadrado amarillo, es otro rectángulo áureo del que calculamos el cuadrado, en color verde y dibujamos un arco de circunferencia con centro en el ángulo superior izquierdo de dicho cuadrado verde, inicio en el vértice inferior izquierdo y final en el vértice superior derecho del citado cuadrado de color verde.
Si a la figura completa le quitas los cuadrados de color amarillo y verde te queda otro rectángulo áureo del que determinas su cuadrado y repites las acciones anteriores.
Al final, obtenemos la espiral áurea la que dentro del arte, arquitectura, escultura, etc., tiene aplicaciones dada su armonía y belleza. También en la naturaleza encontramos espirales áureas en las conchas de algunos moluscos.
Es interesante observar la belleza de líneas que esconde un rectángulo áureo.
Veremos al tratar el icosaedro lo útil de los rectángulos áureos.

