Cálculo del Área del Círculo
Continuamos con el mismo modo de cálculo del área de figuras planas sin recurrir a fórmulas aprendidas de memoria.
Dibuja una circunferencia de 3,5 cm. de radio.
Recorta el papel por la línea dibujada, es decir, por la circunferencia y cuando hayas terminado tendrás en tu mano una superficie circular o la superficie o la parte del plano (papel) limitada por la circunferencia.
¿Podemos considerar a la circunferencia como a un polígono de muchos lados?
Por supuesto que sí. Veamos como lo demostramos.
Dibujo una circunferencia de 3,54 cm., de radio.
Dentro de la circunferencia dibujo 20 triángulos con las medidas que ves en el siguiente dibujo:
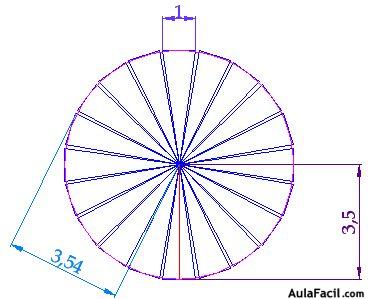
La suma de las bases de los 20 triángulos apenas coinciden con la línea de la circunferencia.
Hemos tomado una parte de la figura anterior y la hemos ampliado al doble de su tamaño:
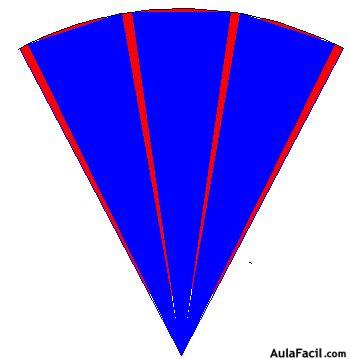
Ves en color azul la superficie de tres triángulos en tamaño doble del de la figura anterior a ella. En color rojo puedes comprobar la superficie que no tenemos en cuenta.
Esto quiere decir que el área del círculo será mayor que el de la suma de todos los triángulos.
El área del círculo será igual a la suma de las áreas de todos los triángulos más las superficies en color rojo.
Calculamos el área de los 20 triángulos:
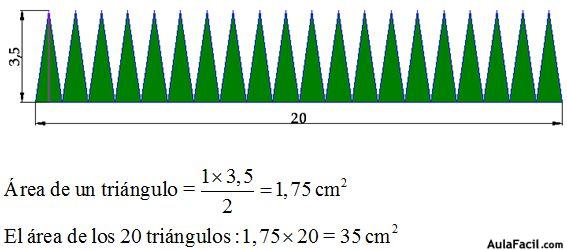
Sería lo mismo que juntar todos los triángulos en uno sólo:
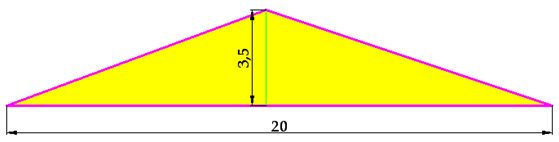
A estos 20 triángulos los puedo transformar en uno sólo siendo la base, la suma de todas las bases y la altura la que es común a todos ellos.
Su área es:
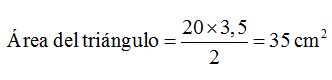
Si introdujésemos dentro del círculo triángulos cuyas bases fueran más pequeñas se aproximarían más a la línea de la circunferencia.
Esto significaría que el área total de todos los triángulos se aproximaría más a la superficie del círculo.
En lugar de dibujar 20 triángulos de 1 cm., de base y 3,5 de altura vamos a comprobar con 44 triángulos de 0,5 cm., de base y la misma altura 3,5 cm:
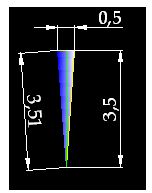
En la siguiente figura compruebas el resultado. Tenemos 44 triángulos de 3,5 cm., de altura con una base de 0,5 cm., dentro de una circunferencia:
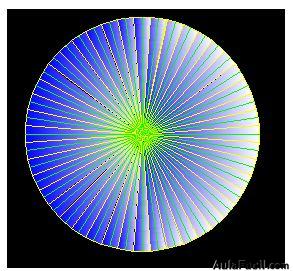
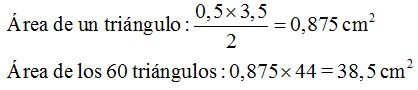
Verás que al aprovechar mejor los espacios nos quedaban entre un triángulo y otro cuando dibujábamos 20, la superficie medida se ha incrementado desde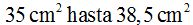 
Ahora la línea formada por los 44 triángulos dan la longitud de la circunferencia de un modo más exacto de cuando lo hacíamos con 20 triángulos de 1 cm., de base.
¿Cómo calculamos con exactitud el área de un círculo?
En el caso de los 44 triángulos tendríamos que la base del triángulo que engloba a todos ellos tendría :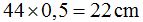 
y la altura sería la misma, 3,5 cm.
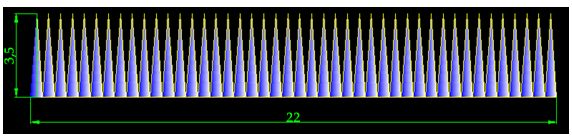
Transformo la figura anterior en un solo triángulo con su misma superficie:
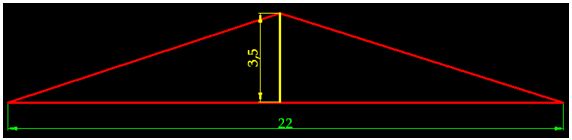
El área de este triángulo vale: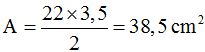 
A pesar de haber incrementado el número de triángulos a 44, las bases no forman una línea curva perfecta, hay una pequeña diferencia que lo puedes comprobar en la siguiente figura donde una parte la hemos ampliado hasta 8 veces:
Notarás que no coinciden las líneas blancas con las rojas. Esto quiere decir que el área del círculo tiene que ser algo superior al área de los 44 triángulos.
¿Cómo solucionamos el cálculo del área del círculo?
De un modo muy sencillo.
En el caso de los 44 triángulos hemos calculado que el perímetro, es decir, la suma de las longitudes de esos triángulos es de 22 cm.
En lugar de tomar como base del triángulo el perímetro de los 44 triángulos, tomamos como perímetro o longitud de la base, la longitud de la circunferencia que sabemos que es de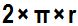 
. Pero ahora no tenemos que tener en cuenta la altura del triángulo sino el radio de la circunferencia que es el lado del triángulo y vale 3,51 cm.:
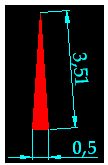
Porque la altura es la perpendicular a la base del triángulo y el lado del triángulo será algo mayor que su altura.
A partir de aquí tenemos un triángulo que tiene por base, 3,51 cm., y por altura: 3,51 cm.
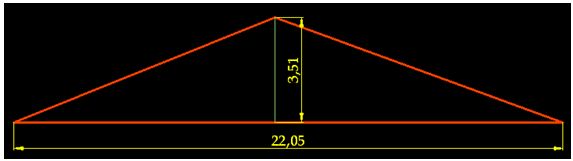
El área exacta del círculo de 3,51 cm., de altura y 22,05 cm., de base:
Notarás una pequeña diferencia entre calcular el área del círculo por medio de triángulos y calcularlo tomando como base del triángulo ÚNICO el de la longitud de la circunferencia y el radio o uno de los lados iguales del triángulo.
La diferencia es de: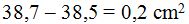 
Cuando tenga que calcular la superficie de un círculo lo puedes hacer considerándolo como un triángulo en que la base es la longitud de su contorno o circunferencia y la altura el valor del radio:
15(2).23 Calcula el área de la figura en color gris. Las medidas las tienes acotadas en la misma figura:
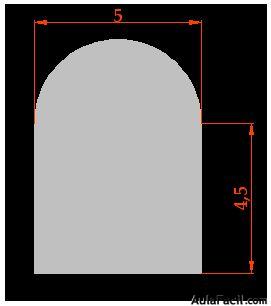
Respuesta: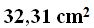 
Solución:
Tenemos un semicírculo de radio 2,5 cm. (mitad del diámetro que es 5) y un rectángulo de 5 cm., de largo por 4,5 cm., de alto o ancho:
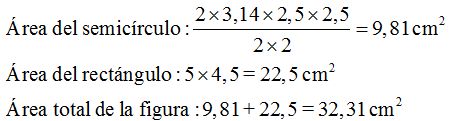
15(2).24 En la figura siguiente tienes un jardín que has de tener en cuenta las siguientes partes y medidas en metros:
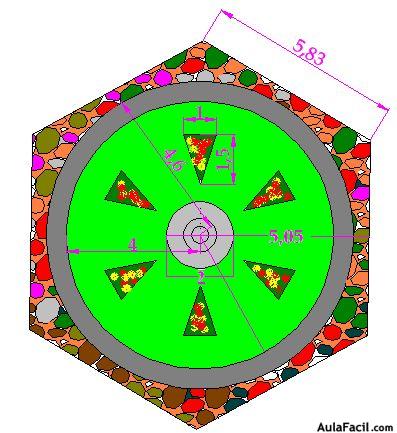
1.- La parte exterior tiene forma de hexágono rellena de piedras planas.
2.- Un paseo circular en color gris
3.- Zona de césped de hierba (color verde)
4.- 6 pequeñas superficies triangulares con rosas rojas y amarillas en el césped
5.- Una fuente central en color gris.
¿Cuál es la superficie de:
a) Suelo con piedras planas
b) El paseo circular (color gris)
c) El césped
d) Los rosales
e) La fuente central?
Respuestas:
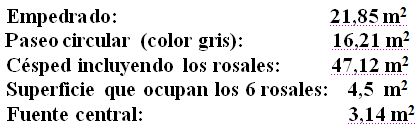
Comprobación:
Si todo el jardín fuese un hexágono su área sería:
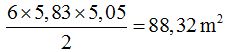
Si a esta superficie le quitamos el círculo mayor que marca el paseo obtendríamos el área de la parte empedrada:
Área del círculo mayor del paseo:
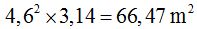
Si al área total le quitamos el área del círculo mayor del paseo nos queda la superficie del empedrado:
Hallamos el área del círculo menor del paseo:
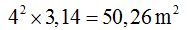
La diferencia de los dos círculos que componen el paseo nos dará el área del mismo:
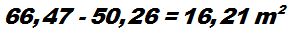
Si al área formada por el círculo menor del paseo le quitamos el área que ocupa la fuente obtenemos el área del césped incluidos los 6 rosales:
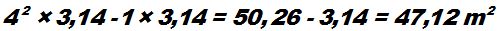
Área de los 6 rosales:
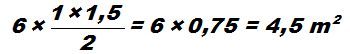
Área de la fuente central:
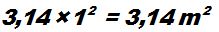
La suma de la parte empedrada más el área del paseo circular más la zona de césped que contiene a los 6 rosales más el área de la fuente: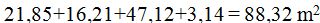 
, como ves, coincide con el área considerando que todo el jardín fuese un hexágono.
