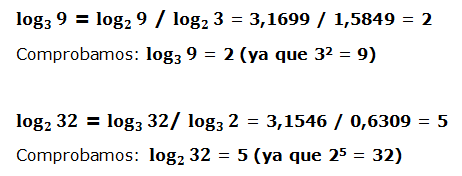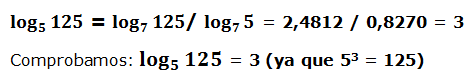Operaciones con logaritmos
a) Suma y resta de logaritmos
La suma (resta) de dos logaritmos de la misma base es igual a un logaritmo de la misma base cuyo argumento es el producto (división) de los logaritmos que se suman (restan).
log b a + log b c = log b (a x c)
log b a - log b c = log b (a : c)
Veamos un ejemplo:
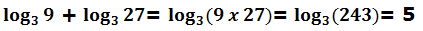
Podemos comprobarlo:
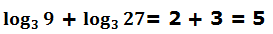
Veamos otro ejemplo:
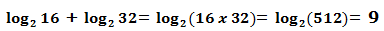
Podemos comprobarlo:
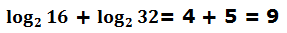
Un tercer ejemplo con la resta:
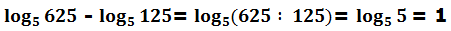
Podemos comprobarlo:
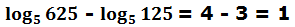
Veamos un nuevo ejemplo con sumas y restas:
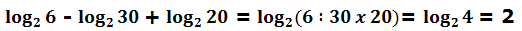
Esta regla que estamos viendo se puede aplicar en sentido inverso: el logaritmo de un producto (división) es igual a la suma (resta) de sus logaritmos.
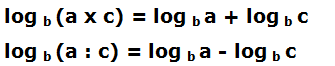
Veamos algunos ejemplos:
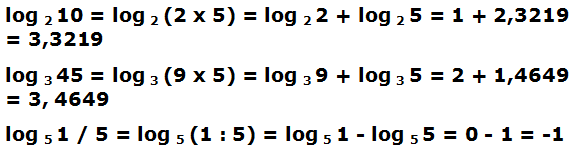
(Atención: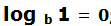 
; el logaritmo en cualquier base de 1 es cero ya que cualquier número elevado a 0 es igual a 1)
b) Logaritmo de una potencia
El logaritmo de una potencia es igual al exponente de la potencia multiplicado por el logaritmo de la base.
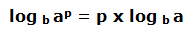
Veamos unos ejemplos:
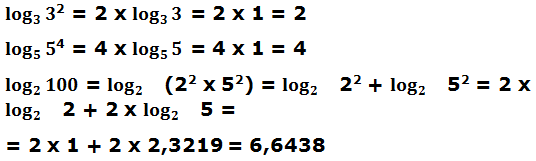
c) Logaritmo de una raíz
El logaritmo de una raíz es igual a 1 dividido por el índice de la raíz y multiplicado por el logaritmo del radicando.
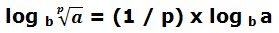
A esta conclusión también hubiéramos llegado transformando la raíz en una potencia cuyo exponente sería 1 dividido por el índice de la raíz.
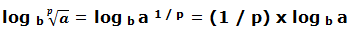
Veamos unos ejemplos:
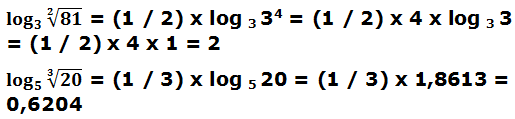
3.- Relación entre el logaritmo decimal y el logaritmo en base b
El logaritmo de un número “a” en base “b”:
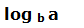
Es igual al logaritmo decimal del argumento dividido por el logaritmo decimal de la base.
Veamos algunos ejemplos:
4.- Relación entre logaritmos de distintas bases
La relación anterior es extrapolable a logaritmos de distintas bases:
El logaritmo de un número “a” en base “b”:
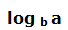
Es igual al logaritmo en base “c” del argumento dividido por el logaritmo en base “c” de la base.
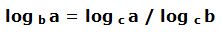
Veamos algunos ejemplos:
