Resta de Fracciones
La resta de fracciones se lleva a cabo dependiendo del tipo de fracción que se nos presente.
Resta de fracciones propias e impropias de igual denominador
La resta de fracciones más sencilla es aquella donde los denominadores de cada fracción tienen en común el mismo número, ya que el proceso de la resta se basa en restar los numeradores y dejar el mismo denominador.
Ejemplo:
Resta de fracciones propias e impropias de diferentes denominadores
Para restar fracciones de distinto denominador debemos seguir el proceso que se indica a continuación:
- Encontrar el común denominador (mcm).
- Dividir el común denominador entre el denominador de cada una de las fracciones y multiplicar el resultado de cada división por su correspondiente numerador.
- Anotar el resultado.
- Restar todos los numeradores y escribir el denominador obtenido en el paso 1.
Ejemplo:
Resolver la siguiente Resta de fracciones:
Pasos
1.- Encontrar el común denominador.
Cuando necesitamos encontrar el denominador común utilizamos el procedimiento del Mínimo Común Múltiplo.
Calculando el común denominador de la resta de fracciones anterior:
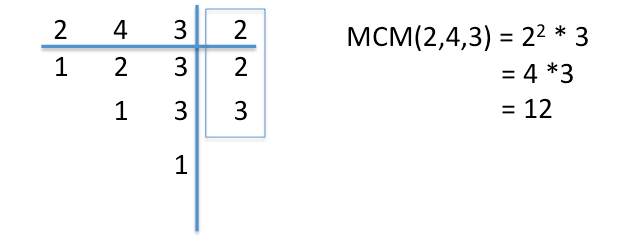
En esta resta de fracciones el valor del nuevo denominador es 12, y los denominadores de la resta de fracciones son 2, 3 y 4.
Si dividimos 12 entre cada denominador, nos daremos cuenta que en todos ellos el residuo es cero.
Ahora nos toca:
2.- Dividir el común denominador entre el denominador de cada una de las fracciones.
3.- Multiplicar el resultado de cada división por su correspondiente numerador.
4.- Anotar el resultado como se indica en la siguiente imagen.
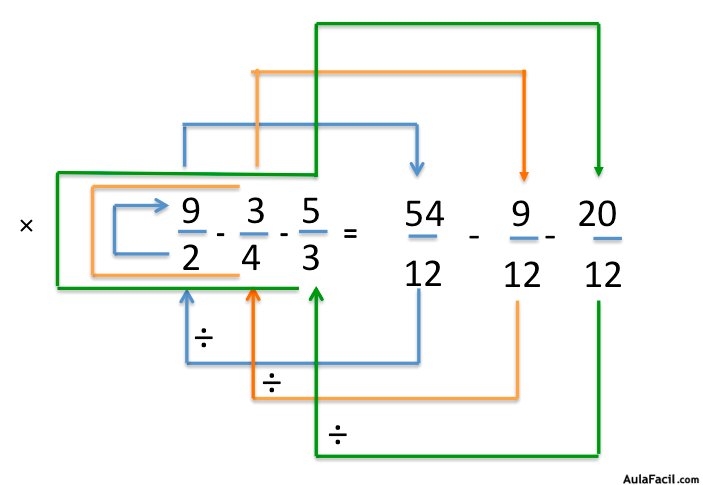
5.- Restar todos los numeradores y escribir el denominador obtenido al calcular el MCM.
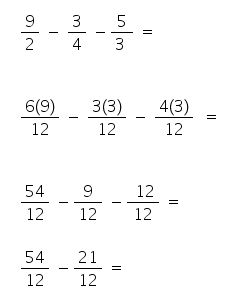
33/12
Resta de fracciones mixtas
El procedimiento más sencillo para realizar la resta de fracciones mixtas es convertir primero la(s) fracción(es) mixta(s) a impropia(s), tal como se explicó en la lección de conversión de fracciones, y posteriormente aplicar el proceso de Resta de fracciones propias e impropias de diferentes denominadores.
Ejemplo:
Resta de fracciones combinadas
En el proceso de resta con fracciones combinadas solo es necesario pasar las mixtas a impropias y aplicar el procedimiento descrito en este documento.
Ejemplo:


