Técnicas de Pronósticos (XIX)
Resumen de pronósticos de juicio.
El peligro en el uso de la mayoría de los métodos de pronóstico que se exponen en este curso consiste en que comprenden la manipulación de datos históricos para generar el pronóstico. Esta práctica es un procedimiento válido si el pronóstico es para el futuro cercano, pero se hace cada vez más sospechosa al incrementarse el horizonte del pronóstico. Los métodos que se abordan son valiosas adiciones al arsenal del pronosticador cuando se considera la particular preocupación de la alta dirección: la predicción a largo plazo del medio ambiente de la compañía.
Diversos autores han fascinado al público en general con sus especulaciones sobre las tendencias de largo plazo actualmente evidentes en nuestra sociedad y el futuro que auguran. Entre los más provocativos se encuentran
Alvin Toffler, El shock del futuro (New York: Random House, 1970). Alvin Toffler, La tercera ola (New York: Bantam Books, 1980). John Naisbitt, Megatrends (New York: Warner Books, 1982). John Naisbitt y Patricia Aburdene, Megatrends 2000 (New York: William Morrow, 1990). Aunque también me fascinan los futurólogos Peter Drucker y de Joel Arthur Baker.
Estos autores poseen una habilidad única para especular sobre el futuro en formas provocativas, sin embargo, las necesidades específicas de pronóstico de un negocio requieren de procedimientos más formales que arrojen proyecciones plausibles de la conformación a largo plazo de su ambiente competitivo.
OTROS ELEMENTOS DE JUICIO EN LOS PRONÓSTICOS
Se han desarrollado diversas técnicas para ayudar a quienes toman decisiones en el proceso de evaluación de información sobre el futuro incierto y tomar las mejores decisiones. Con frecuencia, estas técnicas se abordan en libros de texto y artículos periodísticos bajo el título general de "toma de decisiones", o en ocasiones "toma de decisiones bajo incertidumbre". Cuando los administradores, empresarios e individuos se enfrentan a la tarea de tomar decisiones de frente a lo incierto, su habilidad de pronosticar se convierte en un elemento crítico en el proceso de toma de decisiones.
Cuando se ha concluido el análisis de datos históricos, quien toma las decisiones debe formular un juicio con respecto a las alteraciones en el curso de acción de la empresa. En otras palabras, el analista debe enlazar los resultados del proceso de pronóstico dentro de los procedimientos de toma de decisiones existentes en la empresa. A continuación se exponen brevemente algunos de los elementos de la teoría de decisiones que con frecuencia son relevantes en esta etapa del proceso.
Quienes toman decisiones usan a menudo el concepto de valor esperado, ya sea en forma explícita o implícita. Este concepto comprende el valor promedio que puede tomar tina variable numérica aleatoria a lo largo de varias pruebas. En la tabla 1.13 se presenta una variable aleatoria discreta X en una distribución de probabilidad; se muestra cada valor posible que puede asumir X junto con la probabilidad de cada uno
El valor esperado (esperanza) de una variable aleatoria discreta es el valor promedio que asume la variable aleatoria durante un gran número de observaciones.
Nótese que la suma de probabilidades en la tabla 1.13 es 1.00 o 100%, lo que significa que se ha identificado cada valor posible que puede asumir X. Suponga que la tabla 1.13 representa el número de contratos mayores que una empresa firmará durante el siguiente año fiscal.
Tabla 1.13 Distribución de probabilidad del valor esperado
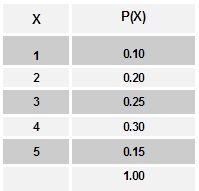
La pregunta que responde el valor esperado es: ¿Cuántos pedidos nuevos pueden esperarse en promedio, si es válida la distribución de probabilidad de la tabla 1.13? La siguiente ecuación se usa para calcular el valor esperado de una distribución de probabilidad como la que se muestra en la tabla 1.13.
E(X) = (X)P(X)
En donde:
E(X) = valor esperado o esperanza
X= valores que puede asumir la variable aleatoria
P(X) = probabilidad de ocurrencia de cada X
Se puede calcular el valor esperado de la tabla 1.13 mediante la ecuación de la manera siguiente:
E(X) = 1(.10) + 2(.20) + 3(.25) + 4(.30) + 5(15) = 3.2
El valor esperado de la distribución de probabilidad de la tabla 1.13 es 3.2. Si en este ejemplo X representa el número de contratos mayores para el próximo año fiscal, se podría decir que, en promedio, si se repitiera muchas veces esta misma distribución, se firmarían 3.2 nuevos contratos. Nótese que no es posible el valor 3.2 en cualquier año; sólo son posibles los valores enteros (1, 2, 3, 4, 5). No obstante, el valor 3.2 representa el valor promedio de la distribución a lo largo de muchos intentos. Es frecuente que quienes toman decisiones se interesen en dichos valores esperados y los utilicen como su mejor expectativa de variables numéricas críticas en la planeación del futuro incierto.
Todos los que toman decisiones utilizan los conceptos de la teoría de la utilidad sobre una base diaria, tanto para decisiones personales como de la organización. Sin embargo, pocos se dan cuenta de que la teoría de la utilidad se ha estudiado formalmente y que su uso puede mejorar el proceso de toma de decisiones. La teoría de la utilidad reconoce formalmente las cantidades en dólares que no pueden juzgarse simplemente observando sus valores. Se debe considerar también en la empresa el impacto de diversas cantidades en dólares. En la tabla 1.13 se calculó que el valor esperado sería 3.2.
