Técnicas de Pronósticos (VI)
MÉTODO DE LA CORRELACIÓN Y TENDENCIA.
Bajo esta denominación se le conoce al enfoque que pretende explotar el grado de linealidad, o alejamiento de ésta, de una determinada serie, como ingrediente básico para proyectarla. Para este propósito es menester introducir algunos conceptos básicos, como el de correlación lineal entre dos variables.
Se entenderá por correlación lineal entre dos variables “X” y “Y” (con el mismo tamaño o magnitud) al grado de dependencia lineal entre ambas.
Se mide mediante el coeficiente “r”, o coeficiente de correlación lineal de Pearson, que se define como:
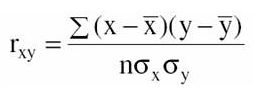
Su valor oscila entre -1 y 1. En otras palabras, r se encuentra en el intervalo abierto:
- 1 =< r <= 1
La interpretación de este coeficiente es muy importante en el análisis de regresión, y en particular en este enfoque. Por tal motivo conviene adelantar algunas precisiones sobre su comportamiento.
Cuanto más cercano de la unidad se encuentre su valor, mayor será la correlación o dependencia lineal entre las dos variables involucradas, respecto de una línea recta con pendiente positiva. Cuando r adopta el valor de 1, entonces la correlación resulta perfecta y los datos se encuentran alineados sobre una misma recta con pendiente positiva e igual a 1. Por el otro lado, cuando más cercano se encuentra r de -1, más cercanas estarán las observaciones respecto de una recta con pendiente negativa, y en el caso extremo, todos los datos estarán alineados sobre una recta con pendiente -1. Cuando r adopta el valor cero, ello implicará que las observaciones poseen un patrón difuso o no relacionado, que no permite identificarlo bajo ninguna tendencia. Empíricamente, cuando el valor de r es mayor que 0.85 consideramos que existe buena correlación entre las variables involucradas.
Un segundo estadígrafo que consideramos también relevante mencionar a estas alturas, es el coeficiente de determinación simple (R2), que se define en forma general como:
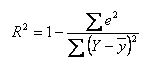
O en forma más sencilla, como el cuadrado del “coeficiente de correlación”, así:
R2 = r2
El coeficiente de determinación, r2 establece la proporción de la variación total en la variable dependiente Y que está explicada por o se debe a la variación en la variable independiente X.
El coeficiente de determinación es el cuadrado del coeficiente de correlación, y toma valores de 0 a 1, que se puede expresar de la siguiente manera:
0 =< R2 =< 1
En otras palabras, según esta nueva definición, el coeficiente de determinación (R2) puede calcularse a partir del valor de “r”, motivo por el cual la introducimos. O sea, no es menester, estimarlo mediante su formulación general, sino que puede trabajarse en conjunto con el coeficiente de correlación. Su importancia radica en que su valor mide la bondad de ajuste global de un modelo respecto de una línea recta estimada mediante el método de mínimos cuadrados.
Mientras más cercano se encuentre su valor de 1, el ajuste global del modelo será casi perfecto, y mayor confianza tendremos en el mismo para fines predictivos, por ejemplo. Y cuanto más cercano se encuentre de 0, más deficiente será su ajuste global, y menor confianza debemos tener en este modelo para el mismo propósito ya mencionado.
Por otra parte, hemos visto que una serie puede adoptar prácticamente cualquier forma. De la infinidad de representaciones gráficas conocidas, existen algunas consideradas como "clásicas". Estas son la lineal, ya conocida, la exponencial, la logarítmica y la asintótica, las cuales se describen a continuación.
