Técnicas de Pronósticos (IV)

Ejemplo 10 del caso 2(a): Aplicaremos un procedimiento alternativo para estimar la TMAC cuando las observaciones corresponden a una variable de conducta irregular (u horizontal) como la que aparece en el cuadro 1.12, comparándolo con el método utilizado anteriormente.

A fin de ilustrar este enfoque, estimaremos, periodo a periodo, la tasa de crecimiento, y posteriormente calcularemos el promedio respectivo. Si lo hacemos obtendremos un valor del 2.2% para la TMAC para todo el periodo (años 1 al 11), como se muestra en el cuadro 1.12.

Cuadro 1.12. Estimación de la demanda de un producto mediante la técnica de la TMAC.

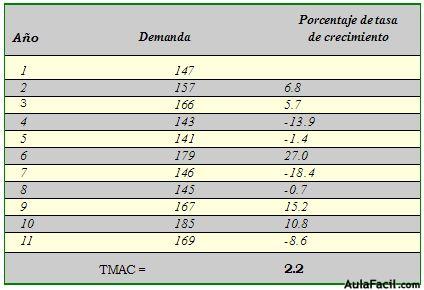
En el cuadro anterior se ha calculado el “crecimiento” o “decrecimiento” de un dato con respecto a su antecesor, y así se ha obtenido el crecimiento o decrecimiento año por año. Por ejemplo, realicemos el análisis para los siguientes años, para corroborar las cantidades y que usted observe el procedimiento:

AÑO 3.

Basándonos siempre en la fórmula de ((Vf/Vi) – 1)100, tenemos que:

((166/157)-1)100 = 5.7%

AÑO 7.

Fórmula: ((Vf/Vi) -1)100

Sustituyendo valores para el año 7, tenemos que:

((146/179)-1)100= -18.4%

Si hubiésemos empleado la metodología del caso 1, tendríamos que la TMAC sería para todo el período:

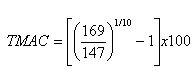
Desarrollando el cociente:

(169/147)= 1.14966

Elevándolo a 1/10 o 0.1:

(1.14966)0.1= 1.014044

Sumando algebraicamente (-1):

1.014044 + (-1)= 0.014044

Multiplicándolo por “100” para obtenerlo como porcentaje:

(0.014044) x 100= 1.4%

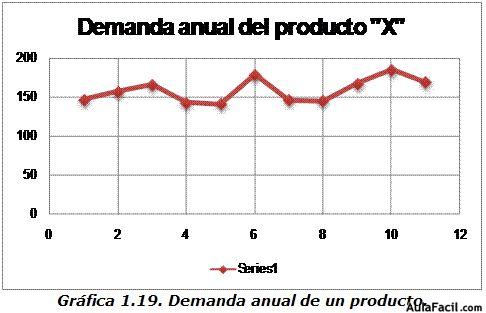
Entonces, comparando ambos métodos, para el año 12 existe una notable diferencia de pronósticos. Nótese que el valor obtenido (1.4%) es totalmente distinto, y podría incluso resultar disparatado frente al obtenido anteriormente (2.2%) y conducirnos a un pronóstico muy alejado de la realidad o poco confiable, si se toma al pie de la letra. Es decir, empíricamente podemos esperar menor precisión en el pronóstico basado en la técnica de la TMAC conforme se incremente el nivel de fluctuación u oscilación de la serie alrededor de los valores observados y pretendamos aplicar a ultranza el enfoque del caso 1 a ciegas o soslayando el patrón o comportamiento físico de la serie. Como ha quedado de manifiesto en los ejemplos discutidos anteriormente.