Análisis de Correlación (I)
Un propósito común en las aplicaciones de pronóstico consiste en examinar la relación entre dos o más variables.
El énfasis en la correlación y la regresión se justifica en virtud del amplio uso de estas técnicas en todo tipo de aplicaciones estadísticas, incluyendo por supuesto, los pronósticos. Además, la ampliación de los conceptos básicos de correlación y regresión en áreas más complejas se consideran en muchos otros procedimientos de pronóstico.
Se supone que las variables bajo investigación son mediciones numéricas, es decir, que se miden mediante un dispositivo o procedimiento que genera números reales en vez de categorías (se utilizan datos de intervalos o escala proporcional).
Diagramas de dispersión.
Un estudio de la relación de variables comienza con el caso más sencillo, el de la relación existente entre dos variables. Suponga que se toman dos mediciones a cada uno de varios objetos. Un analista desea determinar cuál de estas variables medibles denominada Y, tiende a aumentar o disminuir mientras que la otra variable, llamada X, varía. Por ejemplo, suponga que se miden la edad y el ingreso de varios individuos, como se muestra en la Tabla 2. ¿Qué se puede decir acerca de la relación entre X y Y?.
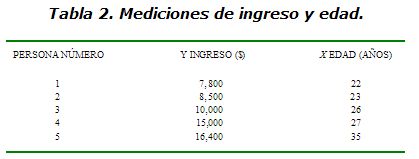
A partir de la tabla 2 resulta aparente que Y y X tienen una relación definida. Al aumentar X, Y tiende también a aumentar. Al observar esta muestra de cinco personas pudiera ser tentador el concluir que entre mayor sea una persona más ingresos tendrá. Desde luego, es peligroso llegar a conclusiones con base en un tamaño de muestra inadecuado, un tema a tratar más adelante. Aun así, con base en las observaciones (n = 5), aparentemente existe una relación definida entre X y Y.
Estos cinco puntos se pueden graficar en una escala de dos dimensiones, con los valores de X en el eje horizontal y los valores de Y en el eje vertical. A esta gráfica se le denomina diagrama de dispersión y aparece en la gráfica 1.10.
Un diagrama de dispersión grafica los puntos de datos X-Y en una gráfica bidimensional, llamada en la mayoría de los casos como “plano cartesiano”.
Un diagrama de dispersión ayuda a ilustrar lo que sugiere la intuición, al observar por primera vez los datos sin procesar, digamos, la apariencia de una relación lineal entre X y Y. A esta relación se le llama positiva ya que al incrementarse X también se incrementa Y.
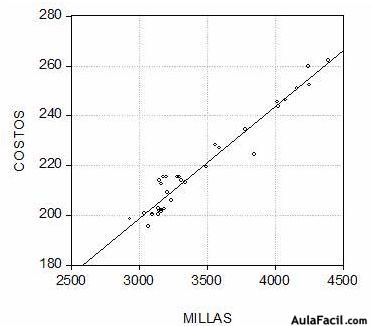
Gráfica 1.10 Diagrama de dispersión de distancia y costos
En otras situaciones que comprenden a dos variables, pueden surgir diferentes patrones de diagramas de dispersión. Considérense las gráficas 1.11.
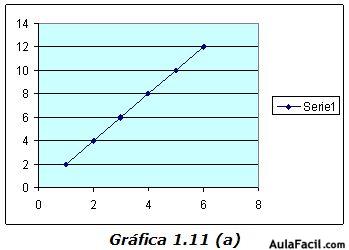
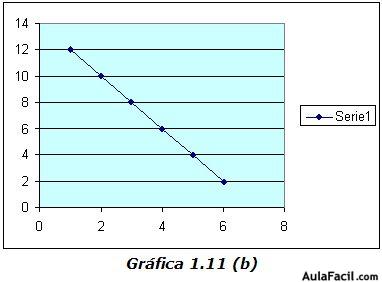
El diagrama 1.11 (a) sugiere lo que se llama una relación lineal positiva perfecta. Al aumentar X, aumenta también Y y en una forma perfectamente predecible. Esto es, que los puntos X y Y aparentemente se ubican sobre una línea recta. El diagrama 1.11 (b) sugiere una relación lineal negativa perfecta. Al aumentar X, Y disminuye en una forma predecible.
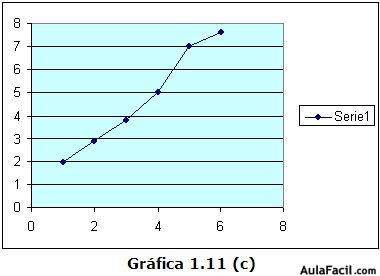
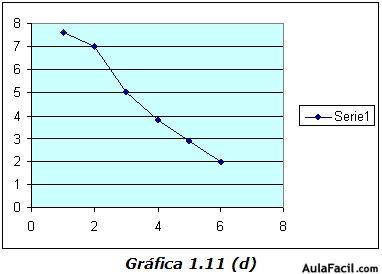
Las figuras 1.11 (c) y 1.11 (d) ilustran relaciones lineales imperfectas positiva y negativa. Al aumentar X en estos diagramas de dispersión, Y aumenta (c) o disminuye (d), pero no de manera perfectamente predecible. De ahí que Y pudiera ser ligeramente mayor o menor que "lo esperado". Esto es, los puntos X-Y no se ubican sobre una línea recta.
Gráfica 1.12. Patrones para las gráficas de datos
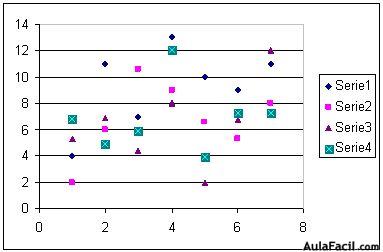
El diagrama de dispersión de la figuras 1.12 sugiere que no existe relación de ninguna clase entre las variables X y Y. Al aumentar X, Y no parece aumentar o disminuir en forma predecible alguna. Con base en la evidencia de la muestra que aparece en el diagrama, se podría concluir que en el universo que contiene todos los puntos X y Y, no existe relación lineal u otra, entre las variables X y Y.
