Historia de los números binarios
La historia de los números binarios se remonta hasta la antigüedad. Nacieron con algunas culturas primitivas. El I Ching es una filosofía china que apareció durante la dinastía Zhoe, hace más de 3000 años, que predica que el Universo está regido por el principio del cambio y la relación dialéctica entre los opuestos, que pone de manifiesto el concepto taoísta del Yin y del Yang.
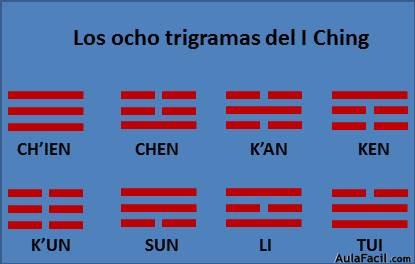
La estructura interna del I Ching se basa en la codificación binaria, y está compuesta por ocho estados de cambio que se conocen con el nombre de trigramas primarios, los cuales se pueden catalogar como un equivalente del ADN Humano. Un trigrama se forma con la combinación de tres líneas horizontales que pueden ser continuas o fuertes (energía Yang, concepto de la masculinidad), o rotas o débiles (energía Yin, concepto de la feminidad). Podemos apreciar los ocho trigramas en la Fig. 7-1
Estos trigramas no son nada más que códigos binario mostrados en un formato gráfico bastante didáctico. Si asumimos que la línea continua equivale a un uno y la línea rota equivale a cero, podemos deducir que cada trigrama tiene el valor binario que se aprecia en la Tabla 7-1, con su correspondiente valor decimal.
| Trigrama | Binario | Decimal |
| CH'IEN | 111 | 7 |
| CHEN | 001 | 1 |
| K'AN | 010 | 2 |
| KEN | 100 | 4 |
| K'UN | 000 | 0 |
| SUN | 110 | 6 |
| LI | 101 | 5 |
| TUI | 011 | 3 |
Tabla 7-1
Como podemos ver, están perfectamente representados los números binarios del 000 hasta el 111, los cuales corresponden a los dígitos del sistema octal al hacer su conversión: 0, 1, 2, 3, 4, 5, 6 y 7.
A pesar de la resistencia de la humanidad para usar un sistema diferente al decimal (recuérdese que al principio dijimos que esto se deba posiblemente a que poseemos diez dedos y la costumbre ancestral de enumerar y hacer cuentas con ellos), poco a poco el sistema binario fue tomando posesión entre las comunidades científicas. Los lenguajes Braille y Morse fueron unas de las primeras aplicaciones de los códigos binarios.
Primero fue el matemático alemán Gottfried Leibniz, quien hacia el año 1703 propuso el Sistema Binario como un medio de realizar cálculos, pues se prestaban para hacerlo de una manera muy sencilla. A mediados del siglo XIX, el también matemático George Boole, de nacionalidad inglesa, intentó usar las técnicas del álgebra para resolver problemas de lógica proposicional mediante procesos que utiliza nuestra mente para sacar conclusiones a partir de unas premisas. Se trata de averiguar si dichos procesos son válidos o no, para determinar si las conclusiones que hemos establecido son verdaderas (lo que se representa con un 1) o falsas (que se representa con un 0).
En la primera mitad del siglo XX, el americano Claude Shanon, ingeniero eléctrico, descubre la manera de utilizar interruptores eléctricos para resolver operaciones aritmético-lógicas, utilizando el álgebra de Boole. Se basaba en dos posiciones de los interruptores: encendido representaba el uno y apagado el cero. Y desde ese momento no hubo forma de parar lo que se venía de una manera arrasadora: la informática.