Problemas de Aplicación de Energía Potencial Gravitatoria

Para resolver problemas que involucran el valor de la energía potencial gravitatoria se debe tener en cuenta el marco de referencia, y definir los valores de energía para ése marco, debido a que la energía es medida a partir de un punto de referencia arbitrario.

En la mayoría de los casos, éste punto de referencia es el piso o superficie plana cercana.

Ejemplo. ¿Qué energía potencial tiene un ascensor de 800 Kg en la parte superior de un edificio, a 380 m sobre el suelo? Suponga que la energía potencial en el suelo es 0.

Se tiene el valor de la altura y la masa del ascensor. De la definición de la energía potencial gravitatoria:

Ug = (800 Kg)*(9.8 m/s^2)*(380 m) = 2,979,200 J = 2.9 MJ

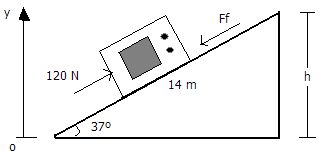
Ejemplo. Un horno de microondas de 12 Kg se empuja para subirlo 14 m de una superficie de una rampa inclinada 37º sobre la horizontal aplicando una fuerza constante de 120 N y paralela a la rampa.

El coeficiente de fricción cinética entre el horno y la rampa es de 0.25. a) ¿Qué trabajo realiza la fuerza sobre el horno?; b) ¿Y la fuerza de fricción?; c) Calcule el aumento de energía potencial del horno.

a) El trabajo de la fuerza está dado por el producto de la magnitud de la fuerza por la distancia desplazada:

W = (120 N) (14 m) = 1680 J

b) El valor de la fuerza de fricción no es un dato dado del problema. Para determinarlo, se debe hacer un DCL:

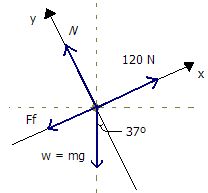
A partir de éste nuevo marco de referencia:

∑Fy = 0 (Debido a que no hay desplazamiento en éste eje).

N - w cos 37º = 0

N = w cos 37º = m * g * cos 37º.

La fuerza de fricción es µk*N, entonces:

Wf = Ff * d = µk * N * d

Sustituyendo:

Wf = µk * m * g * cos 37º * d

Wf = (0.25) (12 Kg) (9.8 m/s^2) (14 m) (cos 37º) = 328.72 J

c) El aumento de energía potencial está dado por:

∆Ug = U(2) - U(1) = m*g*h(2) - m*g*h(1)

Si h(1) = 0 y h(2) = h:

∆Ug = m*g*h

Por trigonometría, sabemos que h = d * sen 37º:

∆Ug = m*g*d*sen 37º

∆Ug = (12 Kg) (9.8 m/s^2) (14 m) (sen 37º) = 990.83 J

Note que los maros de referencia para b) y c) son distintos: cuando se trabaja con energía potencial, sólo interesa datos de altura.

Para el caso de un movimiento vertical con trayectoria curvilínea (movimiento de proyectil, por ejemplo), se debe encontrar la proyección del movimiento en el eje vertical para definir la diferencia de alturas.