Superposición de fuerzas electrostáticas (2)
Ejercicio 1:
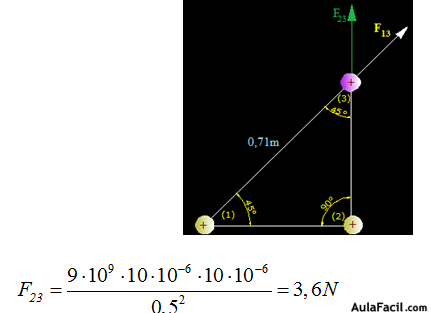
Tenemos tres cargas eléctricas numeradas cuyos valores, distancias y signos los tienes representados en la figura siguiente:
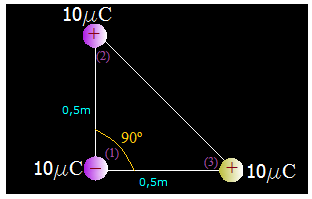
¿Cuáles son las componentes de la Fuerza resultante en función de los vectores unitarios que las cargas (1) y (2) ejercen sobre la (3)?
Respuesta:
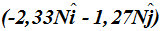
Solución:
Calculamos la Fuerza que la carga (2) ejerce sobre la (3) que vemos que es atractiva:
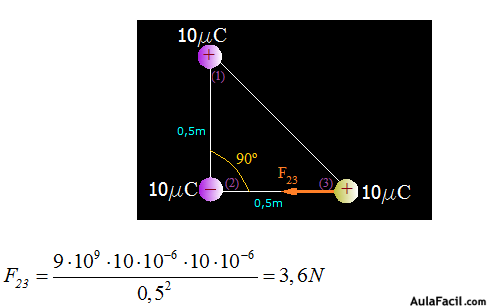
En este momento no tenemos en cuenta el signo.
Calculamos la distancia entre las cargas (1) y (3):
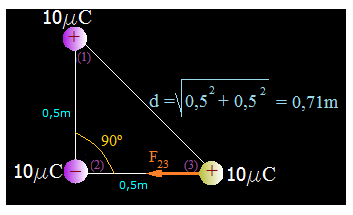
Calculamos la Fuerza repulsiva (F13) que la carga (1) ejerce sobre la (3):
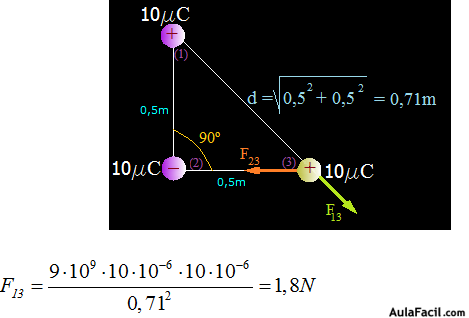
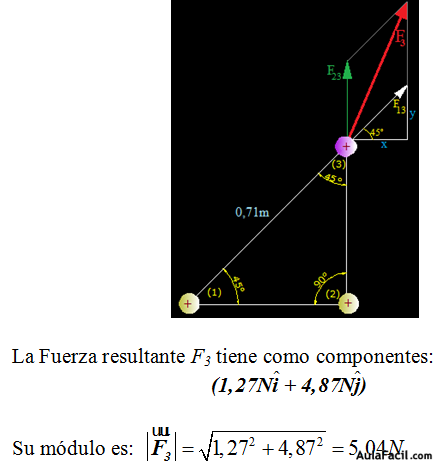
Dibujamos la Fuerza F3 resultante de las componentes F13 y F23:
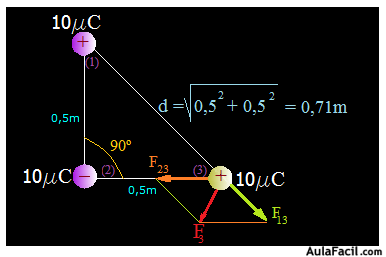
¿Cuál es el total de Fuerzas que en la carga (3) actúan respecto al eje de abscisas (x) suponiendo que en este punto situamos el origen de coordenadas?
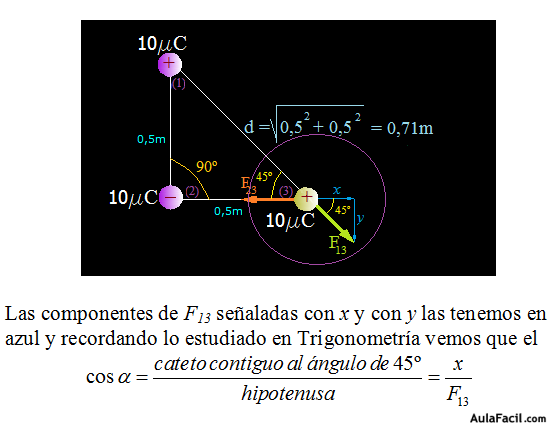
La F23 la tenemos muy clara: –3,6N (ahora tenemos en cuenta el signo y vemos que “apunta hacia la izquierda”), pero la F13 tiene una componente respecto al eje x y otra componente respecto al eje de ordenadas (y).
Vamos a centrar toda nuestra atención en lo que se halla dentro del círculo morado:

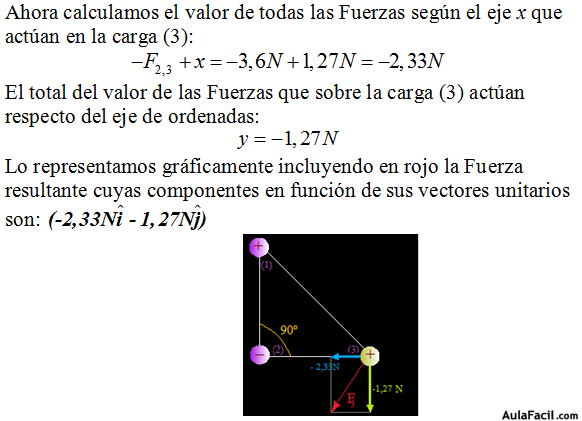
Ejercicio 2:
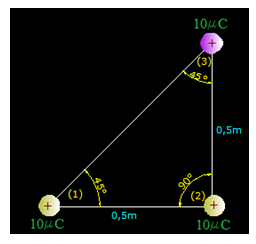
Calcula el módulo de la Fuerza resultante y las coordenadas de sus componentes de dos cargas (1) y (2) actuando sobre la (3).
Los datos los tienes en la figura siguiente:
Respuesta:
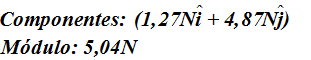
Solución:
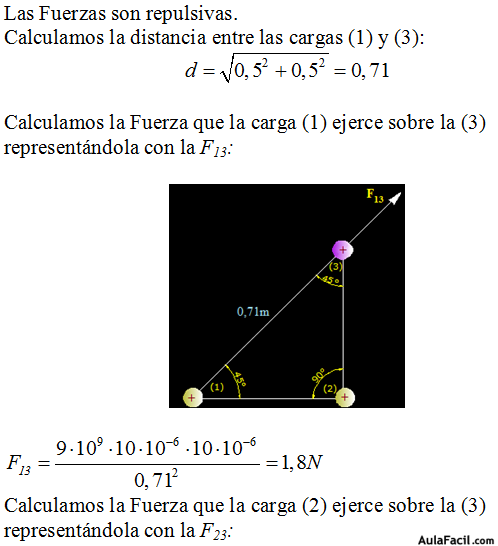

Ejercicio 3:
Cuatro cargas eléctricas de 10 μC cada una y de signos iguales situadas en los vértices de un rectángulo cuyas distancias las tienes en la figura siguiente:
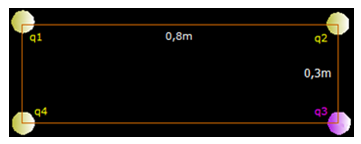
Calcula la medida o magnitud y dirección y sentido de la Fuerza electrostática ejercida por las cargas q1, q2 y q3 sobre la q4.
Respuesta:
Módulo 13,75N en valor absoluto y su dirección 79º respecto al eje x del IV cuadrante.
Solución:
Calculamos la distancia que hay entre q1 y q3 por Pitágoras:
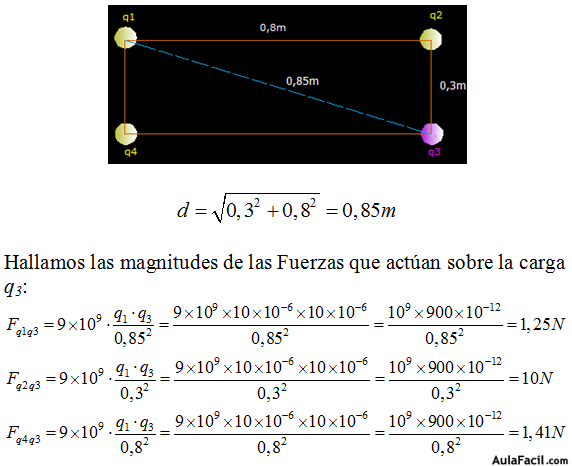
Observa que son magnitudes o medidas de las Fuerzas y no las hemos añadido signo alguno.
Vamos a hallar todas las Fuerzas que actúan sobre la carga q3 en el eje de abscisas:
El valor de la Fuerza que q1 ejerce sobre q3 es repulsiva como las demás porque el texto del problema nos dice que todas las cargas tienen el mismo signo:
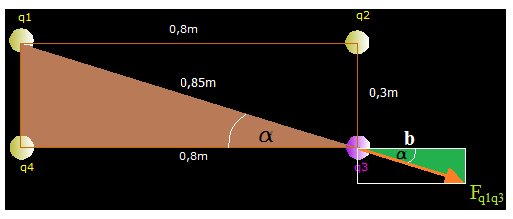

La Fuerza total en el eje x equivale a 1,18 + 1,41 = 2,59N
Ahora vamos a calcular el valor de todas las Fuerzas que actúan sobre la carga q3 respecto al eje de ordenadas.
Es importante que te fijes bien en la figura siguiente en la que resaltamos la componente de Fq1q3 respecto del eje y dentro del círculo azul:
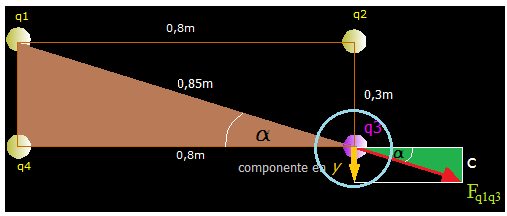
Esta componente no debe quedarnos en el olvido. Ésta y la q2 actúan hacia abajo, es decir, en sentido negativo al establecer en el lugar correspondiente a q3 nuestro sistema de referencia que no es otro que el centro de coordenadas.
Vamos a calcular el valor de la componente vertical de Fq1q3:
Basta que hallemos en el triángulo de color marrón el valor del

Observa que estas dos cantidades son negativas por tratarse de valores de ordenada bajo cero.
Total del valor de estas dos Fuerzas de ordenada negativa: – 3,5 – 10 = – 13,5N
Total del valor de las Fuerzas hacia la derecha es: 2,59N
Total del valor de las Fuerzas hacia abajo es: –13,5N
A estos dos valores los situamos en un eje de coordenadas cuyo centro se halla en q3 y calculando por el teorema de Pitágoras obtenemos la resultante. Todo ello lo tienes en la figura siguiente:
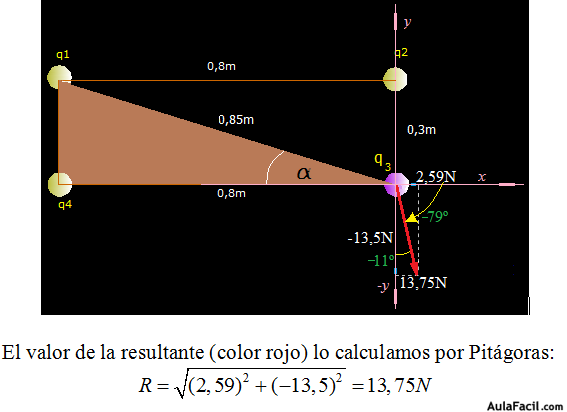

1º) Que la resultante se encuentra en el IV cuadrante, por lo tanto, debajo del origen de coordenadas por ser negativo el valor y.
2º) La resultante forma en el IV cuadrante un ángulo de -79º respecto al eje x.
Conocemos el módulo del vector resultante: 13,75N en valor absoluto y su dirección 79º respecto al eje x del IV cuadrante.
Quizá sea aconsejable recordar la representación de los ángulos negativos en un eje de coordenadas. Si son positivos el sentido para fijar el ángulo es seguir el camino contrario de la marcha de las agujas de un reloj. Si son ángulos negativos siguen la marcha de las agujas de un reloj: