Líneas del campo respecto a la placa metálica
Para nuestros cálculos tenemos en cuenta que las líneas han de ser perpendiculares respecto del área de la placa metálica:
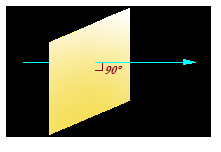
Puede suceder que la línea del campo eléctrico no forme 90º con la placa:
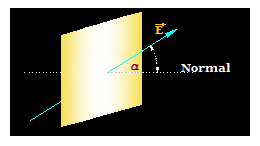
Necesitamos saber el valor de x, es decir, el cateto contiguo al ángulo α:
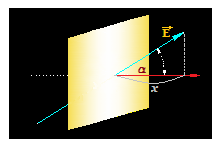
Sabemos por lo estudiado en Trigonometría que:
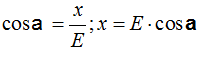
Podemos escribir en este caso que:
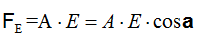
Comprobamos que la cantidad de Flujo a través de una metálica está directamente relacionada con el ángulo formado por ésta y la dirección de las líneas del campo eléctrico.
A mayor ángulo menor Flujo y viceversa.
Ejercicio 1:
Una placa metálica de 0,2m de anchura y 0,5m de altura la atraviesa un flujo de líneas de campo eléctrico de intensidad 10N/C formando un ángulo de 40º entre ambos. Calcula el valor del flujo.
Respuesta:
0,766Nm2/C
Solución:
Ejercicio 2:
¿Cuánto vale el flujo eléctrico cuando la Normal de la placa y la dirección de las líneas del campo son perpendiculares?
Demuestra tu respuesta.
Respuesta:
0
Solución:
Realizamos un sencillo dibujo relacionado con el texto del problema:
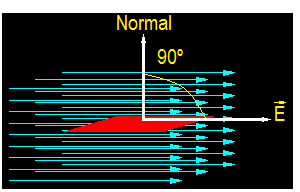
Aplicando la fórmula anteriormente deducida y sabiendo por Trigonometría que el coseno de 90º vale 0 nos queda haciendo la sustitución:
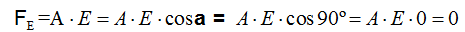
Ejercicio 3:
Una caja metálica hueca se halla dentro de un campo eléctrico ¿qué caras registran flujo eléctrico?
Respuesta:
Caras 3 y 6.
Solución:
Dibujamos un cajón que lo consideramos se halla dentro de un campo eléctrico:
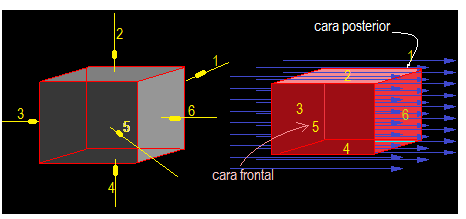
Las hemos numerado.
Por lo estudiado recientemente registran flujo las caras 3 y 6.
Ejercicio 4:
Demuestra que por la cara 5 de la última figura el flujo eléctrico es 0.
Respuesta-Solución:
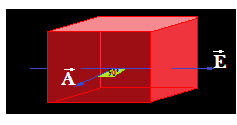
El vector Área (Normal a la cara) y el vector Campo forman un ángulo de 90º y aplicando: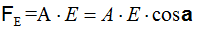 
vemos que coseno de 90º vale 0 lo que significa que el flujo al contener un factor igual a cero el producto es igualmente 0.
Ejercicio 5:
Tenemos un condensador plano cuyas armaduras están separadas 0,10m y cada una tiene 1m2 de superficie.
Entre ellas hemos intercalado un dieléctrico cuya constante es 3.
Si a este condensador le aplicamos 1000V ¿cuál es su capacidad?
Ejercicio 6:
Vamos a construir un condensador de placas cuadradas y la distancia entre ellas equivale a la longitud del lado de cada placa.
¿Cuánto debe medir el lado de cada armadura si queremos que tenga una capacidad de 10-11F y el dieléctrico sea el aire?
Respuesta:
1,13m.
Solución:
Ejercicio 7:
Un condensador tiene una capacidad de 10-4F y se carga en el vacío hasta que adquiere una diferencia de potencial de 500V momento en el que introducimos una placa de vidrio entre las dos armaduras.
Calcula las energías almacenadas en ambos casos suponiendo 6 como valor de ε en el caso del vidrio.
Respuestas:
1ª: 12,5J y 2ª: 2,083J.
Solución:
Ejercicio 8:
Imagina un bloque de acero. Bajo el punto de vista de la Electrostática ¿cómo se distribuyen las cargas?
Respuesta:
Por la superficie.
Solución:
Sea la figura siguiente quien represente a este bloque metálico:
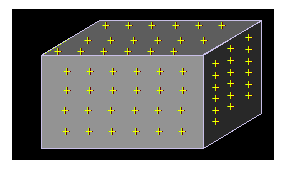
Cuando hablamos de cargas en reposo se distribuyen por la superficie solamente, siempre que el cuerpo sea conductor.
Ejercicio 9:
Un condensador plano tiene una superficie de 1m2 y la separación entre sus armaduras (aire entre ellas) es de 0,1m.
Se le carga a 5000V.
Calcula:
1) Su Carga.
2) Su Capacidad.
3) Su Capacidad con un dieléctrico cuyo coeficiente vale 5.
4) Su Diferencia de Potencial considerando el dieléctrico.
Respuestas:
1) 4,425 x 10-8C
2) 8,85 x 10-12F
3) 4,425 x 10-11F
4) 1000V
Solución:
