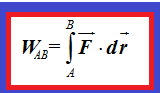Campo eléctrico y campo gravitacional
El campo eléctrico podemos compararlo con el gravitacional.
En el gravitacional tenemos la Tierra con su enorme masa, atrae hacia sí a todos los cuerpos que se hallen en sus proximidades, basta que tengan masa también.
Comparamos las líneas de Fuerza gravitacional con las de un campo eléctrico:
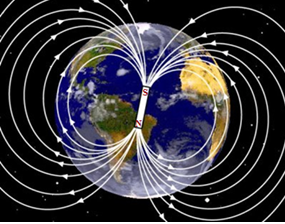
Las líneas en el campo gravitacional salen del polo N magnético ( no lo confundas con el Norte geográfico) y entran por el polo S magnético (no el geográfico).
Las líneas del campo eléctrico salen del polo positivo y entran por el negativo:
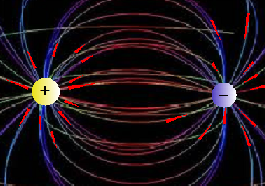
A las líneas de Fuerza del campo eléctrico las podemos representar también:
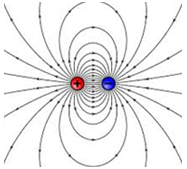
¿Por qué hacemos mención del campo gravitacional al tratar el campo eléctrico?
Anteriormente hablamos de algunas similitudes y ahora nos referimos a otra. Se trata de que en ambos sistemas (gravitacional y eléctrico) las fuerzas son conservativas.
Recuerda que una Fuerza es conservativa cuando el Trabajo (W) que realiza en cuanto a la distancia recorrida se refiere, equivale a la diferencia de las posiciones inicial y final y no de la trayectoria o camino recorridos.
En una trayectoria cerrada el Trabajo (W) es 0.
La Fuerza gravitatoria, recordamos que equivale mg (masa por la aceleración que produce la Tierra).
Si lanzas una pelota hacia arriba, aplicas una Fuerza para que la pelota ascienda. Debes contrarrestar la fuerza de atracción de la Tierra.
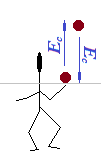
A medida que la pelota asciende, disminuye su Energía cinética (Ec) porque el valor de g la frena, es decir, se produce una aceleración negativa. En cambio, su Energía potencial (Ep) crece mientras va subiendo (aumenta el valor de h) hasta que se detiene para comenzar el descenso.
En el descenso irá aumentando su Ec (+) e irá disminuyendo su Ep(-).
En todo momento la suma de Ec + Ep = 0 siempre que no intervengan otras fuerzas (por ejemplo, las de rozamiento).
La velocidad de partida y de llegada en la última figura, al pasar por la línea horizontal gris serán iguales lo mismo que su Ec vemos que se mantiene, conserva su valor.
La suma de la Energía Cinética que la representaremos con K de ahora en adelante y con U a la Energía Potencial, es decir, la Energía Mecánica, nos da 0 como resultado: K + U = 0 lo que equivale a K = -U.
Todo esto sucede porque la Fuerza gravitatoria es conservativa.
La trayectoria ha sido la misma al subir que al bajar pero de signos opuestos.
Es como si sale del punto A y vuelve al mismo punto A.
A esta trayectoria la denominamos cerrada y significa que la suma de los Trabajos realizados para subir y para bajar son iguales pero de signos contrarios. Todo esto teniendo en cuenta que trabajamos con fuerzas conservativas.
En el caso del campo eléctrico sucede lo mismo, la Fuerza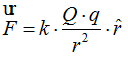 
también es conservativa.
Esto que acabas de leer debes tener muy presente cuando estudiamos el movimiento de una partícula q cargada eléctricamente.
La última figura representativa de las líneas de Fuerza de un campo eléctrico las tienes en dos dimensiones y es sí como vamos a estudiar por estimar que nos va a resultar más fácil.
Lo que sigue procura ir entendiendo perfectamente, sin prisas dado que no es una materia sencilla al principio.
Vamos a estudiarla de dos modos que nos han de conducir a lograr la misma meta que va a ser la de entender, lo mejor posible, conceptos como potencial eléctrico, diferencia de potencial eléctrico y el voltio.
Modo 1:
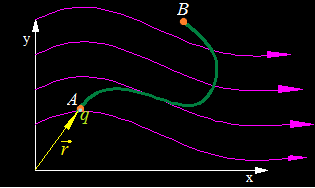
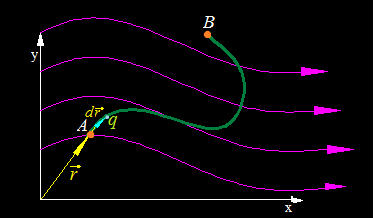
Imagina que tomamos unas pocas líneas de Fuerza del campo eléctrico y las situamos en un eje de coordenadas:
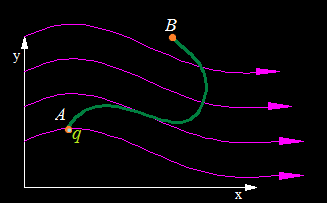
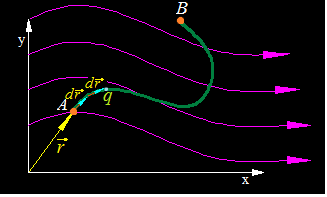
En este eje de coordenadas se encuentra una partícula q cargada eléctricamente y la trayectoria que va a recorrer desde el punto A, donde se encuentra, hasta el punto B porque el campo eléctrico (prescindimos de quién lo provoca ni del lugar donde se halle) va a producir una Fuerza sobre ella que la va a desplazar, y ya sabes, cuando un objeto recorre una distancia por causa de una Fuerza se produce un Trabajo (volveremos a insistir sobre este punto un poco más adelante).
En la siguiente figura dibujamos el vector de posición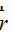 
refiriéndonos al lugar donde se halla la carga puntual eléctrica q y tomando como referencia el origen de coordenadas:
La carga q en una cantidad infinitesimal de tiempo ha recorrido una distancia infinitesimal por causa de la Fuerza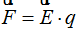 
que la ha impulsado.
Esta Fuerza la ha desplazado a una distancia infinitamente pequeña porque el tiempo en el que esta Fuerza ha actuado también lo ha sido y la representamos por el diferencial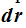 
(como ves echamos mano de lo estudiado en Matemáticas, cálculo infinitesimal).
Así pues, en un tiempo infinitamente pequeño, la partícula ha recorrido una distancia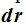 
infinitamente pequeña también:
Ten en cuenta de que si por causa de una Fuerza aplicada a un objeto éste se mueve se produce un Trabajo (W).
¿Recuerdas la fórmula del Trabajo?
Decíamos que cuando aplicamos una Fuerza a un objeto y éste se mueve generamos un trabajo cuya unidad es el julio (joule):
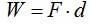(Fuerza por distancia)
(No hemos añadido el factor cos α siendo α el ángulo formado por la dirección de la Fuerza y el desplazamiento del objeto sobre el que hemos aplicado la Fuerza).
En el nuevo lugar de su camino de A a B la carga q se encuentra con una nueva intensidad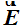 
de campo eléctrico cuyo valor ha experimentado alguna variación sea en módulo, dirección o sentido y q volverá a estar sometida a una nueva Fuerza que la hará moverse otra distancia 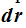produciendo una nueva cantidad de Trabajo:
En cada desplazamiento 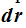que hace q realiza un Trabajo igual a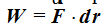 
Esta acción sobre q se repite hasta que llegue al punto B:
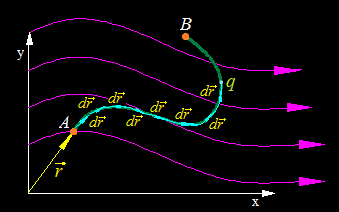
El camino recorrido por la partícula q para ir desde A hasta B es la suma vectorial de todos los sumandos que la representamos gráficamente (color rojo):
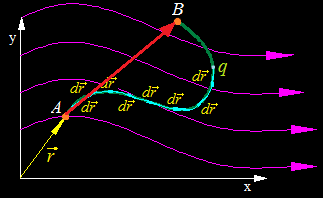
Para nosotros cuenta este vector de posición y no nos importa el caminoque haya recorrido la carga q para ir desde A hasta B, podría haber ido por otro.
¿Qué hacemos para calcular el Trabajo total de la partícula en su desplazamiento desde A hasta B?
Simplemente sumar todos los Trabajos parciales y para eso tenemos las integrales.
Haciendo aplicación de ellas podemos escribir:
