Ecuaciones de Maxwell
No pretendemos hacer un amplio estudio sobre las leyes y ecuaciones de Coulomb, Ampère, Faraday, etc., sino tratar de un modo elemental la existencia de las mismas para que cuando tengas que estudiarlas a fondo, al menos, hayas leído algo sobre ellas.
James Clerk Maxwell es un importante físico y gran matemático nacido en Escocia en el siglo XIX quien entre otros estudios, descubrimientos y experimentos realizó un resumen fundamental para el electromagnetismo que científicos anteriores fueron llevando a cabo dentro de la electricidad y del magnetismo como:
Coulomb, Gauss, Faraday, Ampère, etc.
Podríamos decir de Maxwell que es quien da origen de un modo científico a la creación del electromagnetismo estableciendo así la gran conexión existente entre la electricidad y el magnetismo.
Al Sr. Maxwell le llamó la atención, entre otras muchas cosas, que las fórmulas a las que otros científicos llegaron tenían algo en común.
Se fijó que la fórmula de la Fuerza de gravitación universal estaba dada por la fórmula:
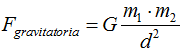 (tenemos en cuenta valores escalares)
(tenemos en cuenta valores escalares)
(constante G por el producto de masas dividida por el cuadrado de la distancia entre ellas).
Observó que la Fuerza eléctrica entre dos cargas viene dada por:
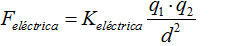
(constante Ke por el producto de cargas dividida por el cuadrado de la distancia entre ellas).
También observó que la Fuerza magnética, en aquellos tiempos se utilizaba la fórmula:
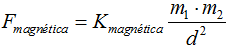
Donde m1 y m2 representan cargas o masas magnéticas debidas a los tamaños de los imanes.
Como ves, tenemos tres Fuerzas:
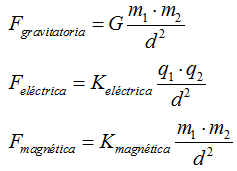
Las constantes G, Keléctrica y Kmagnética a través de estudios, comprobaciones que duraron varios años se dedujeron sus valores:
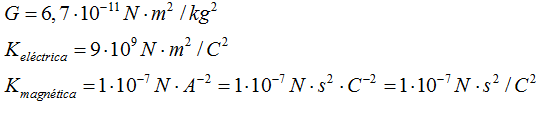
Aclaremos un poco la Kmagnética.
Sabemos que el Amperio es la unidad de Intensidad de la corriente. El Amperio equivale a C (culombio/ segundo) por lo que:
A = C / s
Elevamos al cuadrado los dos miembros de la última igualdad:
A2 = C2 / s2
Hallamos los inversos de esta igualdad: 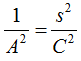 y es lo que figura dentro del valor de la Kmagnética.
y es lo que figura dentro del valor de la Kmagnética.
Maxwell al haber comprobado la relación existente entre el campo eléctrico y el campo magnético quiso ver el resultado de la misma sirviéndose del cociente de las constantes de ambos valores:
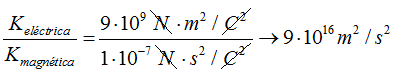
Observa que tenemos metros al cuadrado entre segundos al cuadrado y sabemos que un espacio medido en metros en un tiempo medido en segundos corresponde a la velocidad.
Esto quiere decir que si hallamos la raíz cuadrada de esta última igualdad y llamando c a la raíz cuadrada del cociente obtenemos:
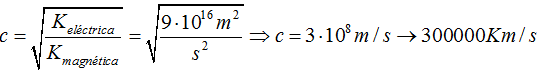
De este modo Maxwell conoció que la velocidad de propagación de las ondas electromagnéticas es la misma que la de la luz.
Otro hecho importante es que Maxwell unifica las leyes que otros importantes físicos realizaron dentro del campo eléctrico y del campo magnético separadamente.
De esta unificación nace la base del electro-magnetismo dando como resultado lo que conocemos como:

