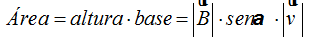Cuantifiquemos lo estudiado
Suponemos que hemos adquirido una idea básica sobre el magnetismo, ahora nos falta saber cómo podemos hacer cálculos que nos permitan conocer diversas magnitudes de algunas variables que utilizamos en este campo de la Física.
Fuerza magnética:
En campo un magnético creado por unos imanes comprobamos fácilmente su existencia de un modo muy sencillo:

Tenemos un tubo de PVC, es decir, un material plástico (se denomina con estas letras por ser un PoliClorurode Vinilo) que utilizamos, por ejemplo, para conducir el agua de riego de un jardín o una parcela de cultivo.
El rayado blanco-negro del tubo no tiene ningún misterio. Simplemente que tenía casi 2mm de diámetro más que el hueco de los imanes y hubo que limarlo.
En la foto (1) vemos tres imanes en la base, los tres tienen el polo N hacia arriba y un cuarto imán con cara N hacia abajo con lo cual se establece una repulsión, está flotando.
La existencia de esta Fuerza de repulsión es evidente. En la foto (2) hemos añadido al imán superior un martillo y una llave inglesa, ambos, de medidas medias y comprobamos que sus pesos no logran, unidos al imán superior, descender hasta contactar con los imanes de la base.
La constatación de la existencia de la Fuerza magnética es muy antigua. Desde hace siglos se viene investigando, comprobando, y trabajando en hallar la fórmula que nos permita determinar el valor de una Fuerza magnética.
Antes de comenzar a realizar cálculos hemos de conocer las variables que vamos a utilizar:

Suponiendo el campo magnético coloreado en color morado difuso, 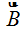 representa a la intensidad del campo magnético en un punto concreto del campo.
representa a la intensidad del campo magnético en un punto concreto del campo.
De un modo paralelo representamos con 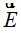 a la intensidad del campo eléctrico cuando estudiamos el curso de electrostática.
a la intensidad del campo eléctrico cuando estudiamos el curso de electrostática.
Piensa que ahora nos encontramos frente a una magnitud vectorial 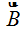 que además de tener un valor escalar dependiendo del lugar del campo magnético donde se halle (no todos los puntos del campo tienen el mismo número de líneas magnéticas), y además, cada campo tiene una dirección. Cuando necesitamos conocer sentidos y direcciones nos encontramos con magnitudes vectoriales.
que además de tener un valor escalar dependiendo del lugar del campo magnético donde se halle (no todos los puntos del campo tienen el mismo número de líneas magnéticas), y además, cada campo tiene una dirección. Cuando necesitamos conocer sentidos y direcciones nos encontramos con magnitudes vectoriales.
Otra variable es q que se refiere a la carga eléctrica que penetra en el campo. Al igual que cuando estudiamos el campo eléctrico imaginábamos una carga (positiva o negativa) la representábamos también con q (se trata de una magnitud escalar, no necesita ni de dirección ni sentido).
De un modo esquemático podríamos representarla:

Esta carga eléctrica debe estar en movimiento para que además de producir un campo eléctrico cree un campo magnético.
Observa que cuando estudiamos el campo eléctrico en Electrostática no hacíamos mención a la velocidad que esta partícula podía tener.
Cuando nos referimos al campo magnético es obligado considerar que la carga eléctrica ha de moverse para generar en su entorno un campo magnético.
Cuanto acabamos de decir significa que esta partícula llega al campo magnético con una determinada velocidad.
Recuerda que la velocidad es otra magnitud vectorial. ¿Por qué es vectorial?
La rapidez con que se mueve puede ser de 8m/s, 29m/s,…es decir, magnitud escalar (lo que señala el cuenta kilómetros del coche), pero la velocidad puede variar en cuanto a dirección y a partir de este momento nos referimos a magnitud vectorial.
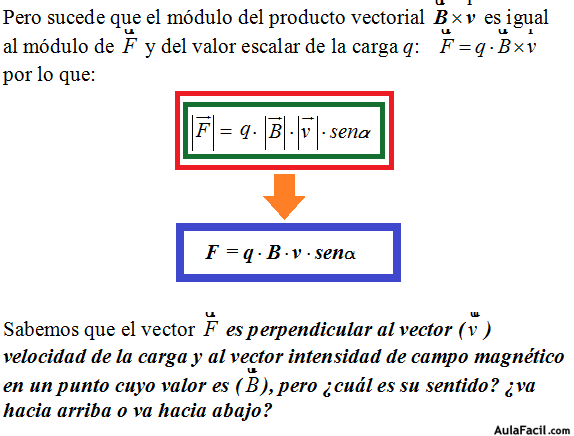
Casi a comienzos del siglo XX, el científico holandés Hendrick Antoon Lorentz tras años de estudio, ensayos y comprobaciones nos dice que la Fuerza magnética que en un campo magnético se produce es directamente proporcional a la carga q, a la 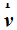 con la que llega y a la intensidad del campo magnético
con la que llega y a la intensidad del campo magnético 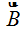 en el punto donde se encuentre q (la carga eléctrica).
en el punto donde se encuentre q (la carga eléctrica).
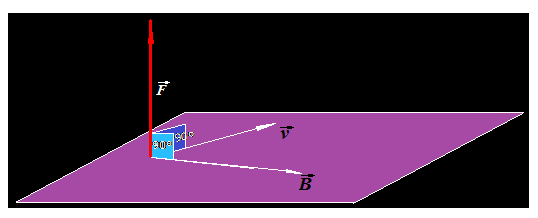
También recordamos que la Fuerza 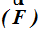 es una magnitud vectorial porque además de conocer su módulo, necesitamos saber su dirección y sentido.
es una magnitud vectorial porque además de conocer su módulo, necesitamos saber su dirección y sentido.
Siguiendo los consejos del premio Nobel de Física (1902) del señor Lorentz decimos que:
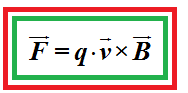
Recordamos de Matemáticas que el producto vectorial de dos vectores situados en un plano:
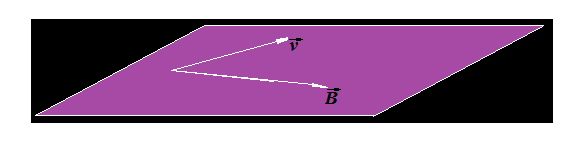
equivale a otro vector que le vamos a llamar  cuya dirección es perpendicular a ambos en su punto de encuentro sobre el plano:
cuya dirección es perpendicular a ambos en su punto de encuentro sobre el plano:
es decir: 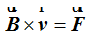
El producto vectorial 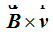 en realidad viene a ser el área del paralelogramo que indicamos con color naranja:
en realidad viene a ser el área del paralelogramo que indicamos con color naranja:
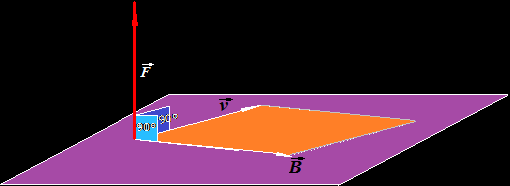
No conocemos la altura de este paralelogramo, trazamos en primer lugar la altura que como sabes es la perpendicular trazada desde un vértice hasta el lado opuesto:
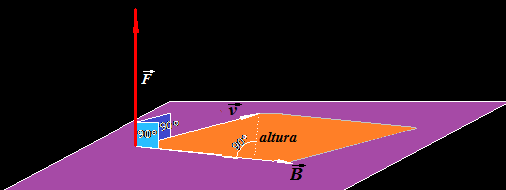
Si hacemos uso de la Trigonometría el lado opuesto al ángulo α de la figura siguiente es la altura:
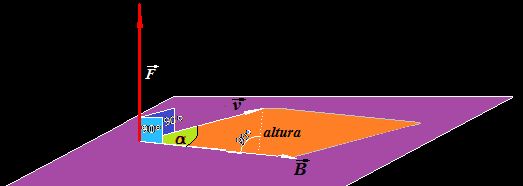
El seno de un ángulo sabes que es igual al cateto opuesto dividido por la hipotenusa: 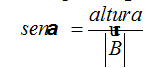
No te olvides que tienes que operar con el módulo del vector. Las operaciones las hacemos con el valor de las magnitudes de los vectores.
El valor de la altura es:
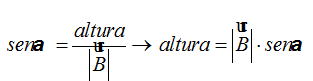
La base del paralelogramo es el vector  .
.
El área de este paralelogramo lo damos con valor escalar, por lo tanto, hemos de tener en cuenta los valores de los módulos.
El área de este paralelogramo podemos expresarlo: