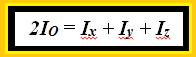Momento de inercia de una masa respecto a un punto 0, lugar donde se cortan los tres ejes perpendiculares de coordenadas
En la figura siguiente puedes ver los tres ejes de coordenadas y una masa m:
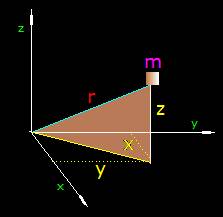
La distancia r entre la masa m y el punto O donde se cortan los tres ejes es una hipotenusa en el espacio que según lo estudiado en Matemáticas sabemos que
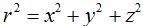
Podemos decir que el momento de Inercia de la masa m respecto al punto O podemos escribir:
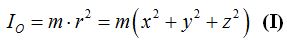
¿Cuál sería el momento de Inercia de dicha masa respecto al eje x?
Es muy sencillo, trazamos una perpendicular desde la masa hasta el eje x tal como lo vemos en la figura siguiente:
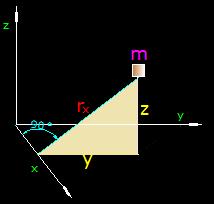
Vemos que la distancia rx es la hipotenusa de catetos y y z por lo que escribimos:
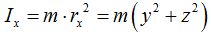
Ahora calculamos el momento de Inercia de la misma masa respecto al eje y:
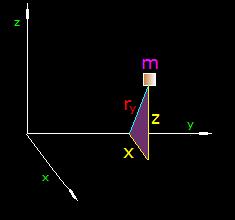
La distancia ry es la hipotenusa de catetos x y z por lo que escribimos:
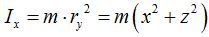
Nos falta calcular el momento de Inercia de la masa m con respecto al eje z:
Dibujamos la figura siguiente:
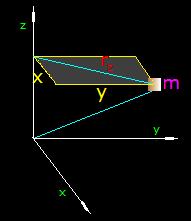
Vemos que la distancia rz es la hipotenusa de catetos y y x por lo que escribimos:
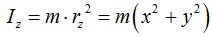
Hemos obtenido las siguientes ecuaciones:
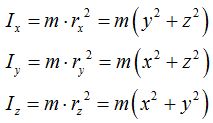
Las sumamos teniendo en cuenta los primeros y terceros términos que al mismo tiempo quitamos paréntesis:
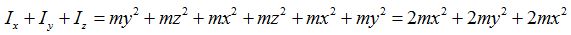
Sacando factor común a 2m: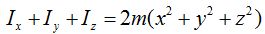 
Sabemos de (I) que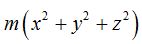 
es igual a IO lo que nos permite escribir:
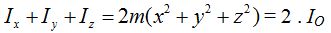
Esta fórmula nos puede ser muy útil en la resolución de algunos problemas:
