Momento de inercia de un cilindro de pared delgada

Lo mismo que en casos anteriores lo deducimos resolviendo el problema siguiente:

2.174  Deduce el momento de Inercia de un cilindro con grueso de pared insignificante de radio R, masa M y una altura H alrededor de su eje central.

Respuesta: IO = MR2

Solución

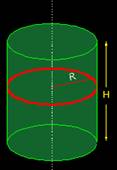
Se trata de un cilindro que está hueco con paredes muy delgadas en el que puedes ver en color rojo un anillo o aro del mismo radio que el cilindro.

Consideramos al cilindro como una suma de infinitos aros de radio R y una altura dh (diferencial de la altura H).

Anteriormente estudiamos que la densidad por unidad de superficie que la representamos por 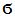la obtenemos de:

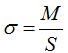
Significa que la densidad de cada partícula equivale a: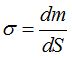

Como 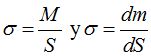  significa que  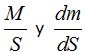también son iguales.

Haciendo operaciones vemos que: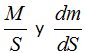

Desarrollando la fórmula del área de cada aro:

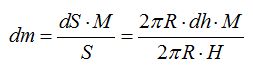
Simplificando:

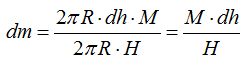
Tomando la fórmula 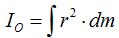 sustituimos valores y resolvemos la integral:

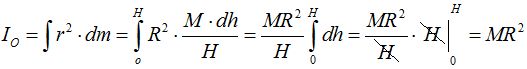
Esta fórmula si recuerdas, coincide con el momento de Inercia de una arandela o un aro.