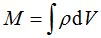Ampliando el concepto de masa en sistemas discretos y continuos
Supongamos una superficie encerrada por la línea amarilla:
En el interior de esta figura existen muchas partículas que las indicamos según indicamos en la figura siguiente:
Suponiendo que a la masa de cada partícula la tenemos numerada, la SUMA de todas las masas en un sistema discreto las escribimos:
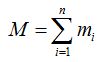
Es decir que la suma total de masas será:
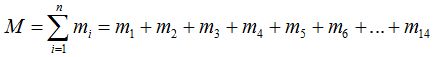
En un sistema continuo cuando el número de partículas es muy elevado utilizamos otro procedimiento teniendo en cuenta el objeto.
La forma del objeto puede ser:
1)-lineal (una varilla)
2)-superficial (un disco)
3)-volumétrica (una esfera)
Sabemos que la Masa(peso) = Volumen por densidad.
- En el caso lineal utilizamos el parámetro λ (lambda) para designar la densidad lineal que será uniforme en toda su longitud (L) y su valor equivale a:
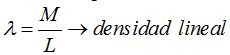
Haciendo operaciones obtengo: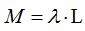 
, por cada partícula.
La masa total la calculamos: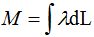 
-
En el caso superficial utilizamos el parámetro
(sigma) para designar la densidad superficial que será uniforme en toda su superficie (S) y su valor equivale a:
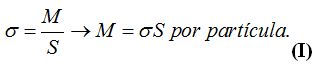
La masa total la calculamos: 
-
En el caso tridimensional utilizamos el parámetro
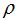(ro) para designar la densidad volumétrica que será uniforme en todo el objeto (V) siendo su valor:
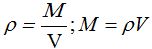por partícula.
La masa total obtendremos de: 
