Composición de fuerzas
1. Composición de fuerzas
Cuando sobre un cuerpo actúan más de una fuerza, la acción de todas ellas se puede remplazar por una fuerza resultante que se obtiene “sumando” vectorialmente cada una de ellas.
Se pueden dar tres casos:
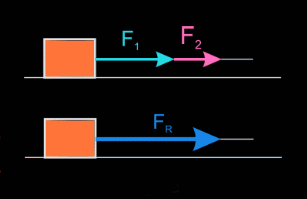
- Fuerzas en la misma dirección y sentido. La fuerza resultante tiene la misma dirección y sentido que las fuerzas componentes, y su módulo es la suma de los de ellas.
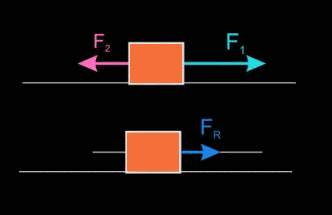
- Fuerzas en la misma dirección y sentidos contrarios. La fuerza resultante tiene la misma dirección que las fuerzas componentes, su sentido es el de la mayor de ellas y su módulo es la diferencia de los de ellas.
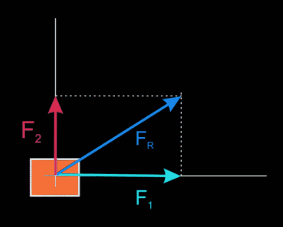
- Fuerzas angulares y concurrentes. No tiene la misma dirección, y la resultante que parte del punto de aplicación de las fuerzas coincide con la diagonal del paralelogramo que forman dichas fuerzas y sus paralelas. Nosotros vamos a considerar sólo el caso particular de fuerzas que sean perpendiculares, es decir que formen 90º entre sí. Por ello, la diagonal coincide con la hipotenusa del triángulo rectángulo. Luego el módulo de esta resultante se calcula aplicando el teorema de Pitágoras:
2. Descomposición de una fuerza
En multitud de ocasiones, para estudiar las fuerzas que actúan sobre un sistema nos resulta muy útil la descomposición de alguna o algunas fuerzas, para después calcular la resultante de todas ellas. Por ello vamos a explicar cómo se descompone una fuerza.
Cada fuerza puede considerarse como resultado de la suma de al menos dos fuerzas concurrentes. Entre las posibilidades infinitas, la única pareja de fuerzas útil a efectos prácticos es aquella que forma 90º y que, para mayor comodidad, situaremos sobre un eje cartesiano:
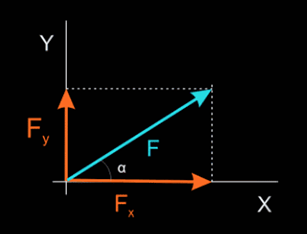
Dado que se forma un triángulo rectángulo, las fuerzas componentes se pueden obtener mediante:
Siendo el ángulo que forma la fuerza (F) a des componer la con el eje OX.
Cuando varias fuerzas actúan sobre un cuerpo y la resultante de todas ellas es nula, se dice que el cuerpo se encuentra en equilibrio.
----0----
Ejercicio:
La resultante de dos fuerzas perpendiculares vale 80 N y forma un ángulo de 30º con la horizontal. Calcular cada una de las fuerzas componentes.
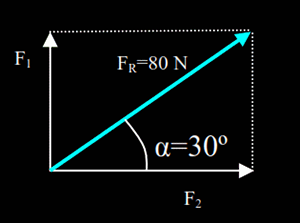
Solución:
Como conocemos la hipotenusa y un ángulo del triángulo y debemos calcular los otros dos lados, utilizaremos la definición de seno y coseno. Es decir: