Análisis Discriminante. Clasificación con 2 grupos
CLASIFICACIÓN CON 2 GRUPOS.
En esta situación, partimos de que la población se divide en 2 grupos o subpoblaciones, G1 y G2, sobre cuyos individuos se observan en general, “p” variables X = (X1, X2...Xy). Y supongamos que, en cada grupo Gf, (f = 1, 2), la variable absolutamente continua X = (X1, X2...Xy)’ se distribuye según una cierta función de densidad de probabilidad fl(x). Además representaremos por “u” y “E” el vector de medias y la matriz de varianzas y covarianzas poblacionales y, análogamente, por u1, u2, E1 y E2 los correspondientes vectores de medias y matrices de varianzas y covarianzas de los respectivos grupos G1 y G2. En estas circunstancias, el Análisis Discriminante trata de establecer alguna regla que relacione características y grupos, de forma que permita la identificación (clasificación) óptima de individuos en función de sus características.
Un criterio muy importante empleado en el Análisis Discriminante, es el criterio de máxima verosimilitud, siempre induce a considerar como solución del problema planteado aquélla que explique con una máxima probabilidad lo que se observa en la realidad. Por tanto, la Regla de Máxima Verosimilitud aplicada al análisis discriminante para identificar (clasificar) un individuo de características x en alguno de los 2 grupos existentes será:
Asignar x al grupo G1 f1(x) f1(x)
Es decir, la regla de máxima verosimilitud asigna el nuevo individuo, que presenta características x, al grupo Gy en el que dichas características presentan la máxima probabilidad o densidad de probabilidad.
Para ilustrar intuitivamente el proceder de esta regla, supongamos que tenemos una única característica unidimensional clasificadora continua de forma que, en los grupos G1 y G2 se distribuya y localice distintamente como aparece en los siguientes gráficos:
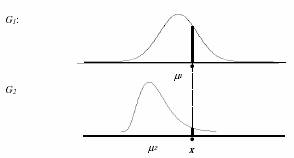
Como observamos en el gráfico, un individuo de característica x presenta una densidad de probabilidad en cada distribución de cada grupo. Así, la característica x del individuo en el grupo G2, se encuentra en una zona muy improbable, por ser mayor de lo común en este grupo. Sin embargo, la característica x del individuo se encuentra en una zona más probable en el grupo G1, ya que se encuentra más cercana a la moda. Así pues, la regla de máxima verosimilitud nos inducirá a asignar los individuos que presentasen la característica x al grupo G1, para el que la densidad de probabilidad en dicho valor de la característica, x, es más alta.
