Análisis Discriminante. Caso particular
CASO PARTICULAR: 2 GRUPOS NORMALES UNIVARIANTES CON IGUAL VARIANZA (k=2, p=1).
En este caso sólo habría dos grupos (k=2) para clasificar a los individuos en función de una única variable x (p=1). Además, supondremos que esta característica clasificadora x se distribuye normalmente en ambos grupos, con igual varianza s pero con distintas u1 y u2.
Si suponemos, sin perdida de generalidad, que u1 u2, la función de densidad de la característica para el grupo G1 se encontraría a la izquierda de la correspondiente función de densidad para el grupo G2, ya que, en el grupo G1 los valores más probables están alrededor de u1 y en el grupo G2, alrededor de u2.
Existen valores de la característica para los que podemos encontrar individuos ubicados en cualquiera de los dos grupos, aunque con distintas verosimilitudes. Así, en la zona sombreada del siguiente gráfico es más probable que el individuo pertenezca al grupo G2 que al G1; mientras que en la zona simétrica es más probable que el individuo pertenezca al grupo G1 que al grupo G2.
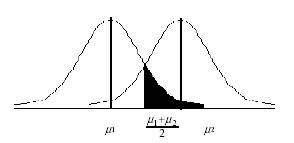
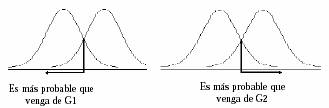
Intuitivamente, de lo dicho hasta aquí, podemos deducir cual será la forma de decidir sobre la pertenencia a los grupos de un elemento que presenta una característica x. El eje de simetría del gráfico pasa por el valor promedio de u1 y u2, y es éste punto el valor crítico que separa las dos zonas de máxima verosimilitud de cada grupo. En la zona de la izquierda es más probable la pertenencia al grupo G1 pues la función de densidad en este grupo es siempre superior a la del G2, y en la zona opuesta ocurre lo contrario. Luego, cualquier individuo con característica a la izquierda de la línea vertical debe ser asignado al grupo G1, y todo individuo con característica a la derecha de esta línea debe ser asignado al grupo G2.
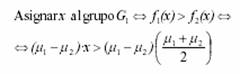
Analíticamente, sustituyendo la densidad de probabilidad en cada grupo Gj, por la expresión correspondiente a la de una distribución normal univariante de media uj y desviación típica s, en la expresión de la regla discriminante de máxima verosimilitud antes definida, ésta quedaría como:
Hasta aquí hemos realizado un repaso de análisis multivariado, espero no haberlo asustado a usted con toda ésta teoría, pero como la idea es que a usted se le quite el miedo a utilizar el programa SPSS, procedemos a continuación a realizar algunos ejemplos de Análisis Discriminante con el software en cuestión.
