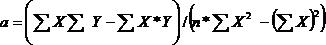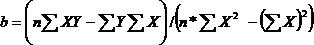Cálculo
Para obtener los valores de los coeficientes se tiene en primer lugar efectuar los productos encontrar sus sumatorias y luego simultanear la ecuación y despejando en cada caso el valor que se requiera:
Precio X | Cantidades Y | (X)(Y) |
| |
3.3 | 2 | 6.6 | 10.89 | |
4.4 | 2.5 | 11 | 19.36 | |
3.3 | 3 | 9.9 | 10.89 | |
5.5 | 4 | 22 | 30.25 | |
4.4 | 3.5 | 15.4 | 19.36 | |
5.5 | 3.5 | 19.25 | 30.25 | |
6.6 | 4.5 | 29.7 | 43.56 | |
6.6 | 5 | 33 | 43.56 | |
7.15 | 5.5 | 39.325 | 51.1225 | |
7.7 | 5.5 | 42.35 | 59.29 | |
7.7 | 6 | 46.2 | 59.29 | |
8.8 | 7 | 61.6 | 77.44 | |
8.8 | 7.5 | 66 | 77.44 | |
11 | 9 | 99 | 121 | |
9.9 | 8.5 | 84.15 | 98.01 | |
TOTAL | 100.65 | 77 | 585.475 | 751.7125 |

Con el coeficiente encontrado se procede a sustituir en cualquiera de las dos funciones originales para despejar el valor de a por lo que se obtiene
585.475 = (a) 100.65+ (b) 751.7125
585.475 = (a) 100.65+ 0.901166978) 751.7125
585.475-667.7418482 = (a) 100.65
-91.94348195/100.65= a
a = -0.913497088
De manera tal que la ecuación queda:
Y(X) = 0.9012 X- 0.9135
A un precio de 0, según esa ecuación, la producción seria -0.91 unidades, la elasticidad precio de la oferta como es de esperarse es positiva en la medida que cambie el precio de la producción este tendrá un impacto en el cambio de oferta a un mayor precio se ofrecerá una mayor cantidad de producto.
Para efectos simplificadores se puede usar de manera general