Tangencias entre circunferencias y rectas

1. Rectas tangentes a dos circunferencias dadas

1.1 Exteriores

Restamos al radio mayor de las circunferencias el radio menor y trazamos la circunferencia resultante.
Unimos O1 y O2 y hallamos la mediana para dibujar la circunferencia que pasa por los dos centros.
Trazamos dos rectas desde O1 que pasen por P y Q y corten en T1 y T2.
Dibujamos paralelas a O1-T1 y O1-T2 con origen en O2, con lo que hallamos los puntos de tangencia T3 y T4.
Unimos los puntos tangentes.

1.2 Interiores

Sumamos al radio mayor de las circunferencias el radio menor y trazamos la circunferencia resultante.
Unimos O1 y O2 y hallamos la mediana para dibujar la circunferencia que pasa por los dos centros.
Trazamos dos rectas desde O1 que pasen por P y Q y corten en T1 y T2.
Dibujamos paralelas opuestas a los segmentos O1-T1 y O1-T2 con origen en O2, con lo que hallamos los puntos de tangencia T3 y T4.
Unimos los puntos tangentes de las dos rectas.

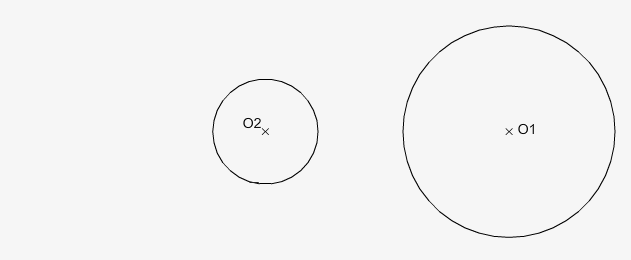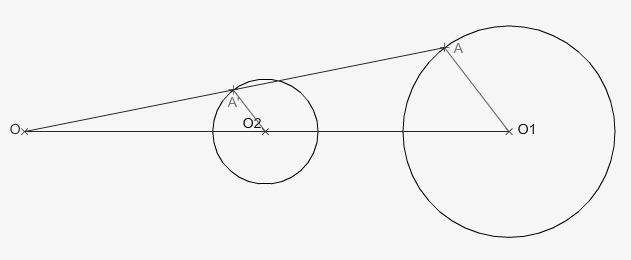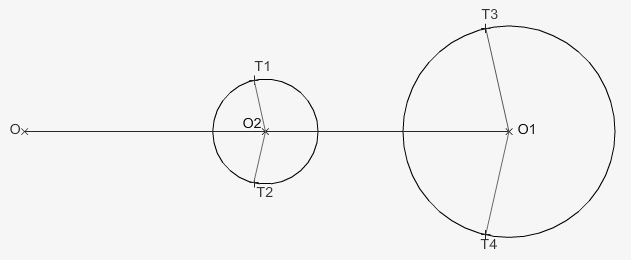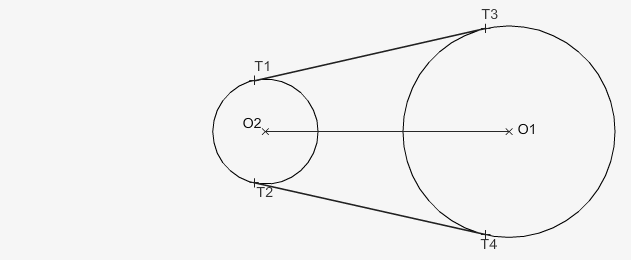
1.3 Exterior aplicando homotecia

Desde O1 dibujamos una línea cualquiera que corte en A y trazamos una paralela a esta que pase por O2 para hallar A'. Unimos A-A' y O1-O2 con dos rectas que se corten en O que es nuestro origen de homotecia.
Desde O trazamos una circunferencia que pase por O2, con lo que hallamos los puntos de tangencia T1 y T2.
Trazamos dos paralelas a los segmentos O2-T1 y O2-T2 con origen en O1 y hallamos T3 Y T4.
Unimos los puntos y dibujamos las rectas tangentes.

2. Circunferencias tangentes a rectas

2.1 Tangente a dos rectas que se cortan dado un punto de tangencia

Trazamos la bisectriz del ángulo formado por las dos rectas.
Desde el punto de tangencia dado T1 trazamos una perpendicular que corte a la bisectriz en O.
Trazamos la circunferencia tangente con centro en O que pasa por T1.

2.2 Tangente a tres rectas que se cortan

Hallamos las bisectrices de al menos dos ángulos formados por las tres rectas y hallamos O.
Desde cualquiera de las tres rectas trazamos una perpendicular que pase por O y hallamos T1.
O es el centro de la circunferencia tangente que pasa por T1, T2 y T3.