El sistema del cuadrado y del triángulo

(64) Finales de Peones.
(Ilya Maizelis)
(Los comentarios han sido retomados de Ilya Maizelis, de su libro "Finales de Peones").

Las posiciones con dos puntos de ataque no son sólo posibles en éste, sino en cualquier otro sistema de casillas conjugadas. La maniobra de los reyes en estas posiciones no viene determinada de ningún modo por la forma que presente el zugzwang. Puede tener características de oposición como en el ejemplo anterior. Los reyes pueden mantenerse en columnas vecinas como en este ejemplo. La maniobra puede ser también mixta (combinada) y hasta completamente distinta de las dos indicadas, como se aclarará más adelante.

El quid de la cuestión estriba en que el tipo de la maniobra depende en cada caso concreto de las características de la estructura de los peones, es decir, del sistema de casillas críticas que corresponde a esta estructura. Consideremos el fundamento teórico de la maniobra de los reyes en las posiciones con dos puntos de ataque. En la posición de análisis (V. Leik, 1941), se halla muy distante de ser el primero en este sentido y su concepción tampoco es original, ya que la idea tiene precedentes. No obstante, en esta posición es cómo da para el estudio, gracias a su sencillez y a que está desprovista de grandes zonas de conjugación.

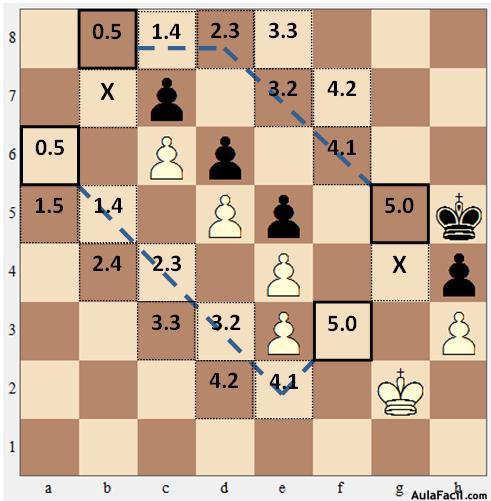
El diagrama se caracteriza por los puntos de ataque (casillas críticas) g4 y b7 y sus correspondientes zugzwangs: Rf3-Rg5 y Ra6-Rb8. Los caminos más cortos entre las posiciones de zugzwang constan, para uno y otro adversario, de seis escaques (los de las blancas f3-e2-a6); y los de las negras (g5-d8-b8). El rey negro debe mantenerse una columna a la derecha del blanco.

El concepto del camino más corto fue establecido por R. Bianchetti en 1925, la hacer el análisis de una posición. El señaló cada casilla con dos cifras que indicaban las distancias que le separaban de la primera y de la segunda posición de zugzwang. Aquellos escaques en los que ambas cifras coincidían los consideraba "conjugados". En 1931, K. Ebersz adoptó esta numeración de las casillas para construir su teoría matemática (en gran parte abstracta) de la maniobra de los reyes, basada en el sistema de coordenadas. El final de su artículo (las conclusiones) no fue publicado.

En 1952, A. Chéron se aprovechó de la ingeniosa idea de Bianchetti, pero con el único fin de escoger por su mediación las casillas conjugadas más eficaces entre todas; a partir de este momento señaló las zonas conjugadas por letras. Las distancias que separan las casillas de los puntos de ataque (distancias "críticas") se ven inmediatamente en el tablero, y esto parecía que debiera dar al jugador el punto de orientación que le es tan necesario en las complicadas maniobras de los reyes.

Sin embargo, como se verá más adelante, y sin dejar de reconocer cierta utilidad en las consideraciones que acabamos de exponer, no deja de ser dudoso el que sobre esta base sea posible crear un método completo para resolver posiciones bloqueadas. Las casillas del camino más corto han sido marcadas en la posición de análisis con cifras que señalan sus distancias (número de jugadas) al punto de zugzwang izquierdo, primero, y después al derecho.

Estas casillas corresponden exactamente a las análogas del adversario y, en este caso, pueden ser consideradas como zonas principales. En caso de que el rey blanco se situase en uno de los escaques del camino más corto, el rey negro deberá responder haciendo lo mismo, precisamente porque el camino es el más corto. En muchas posiciones, el método a seguir para ganar consiste en obligar al rey contrario a situarse en una de las casillas de su camino más corto y, después de esto, ocupar la casilla conjugada de su camino más corto.

En la posición de análisis el problema es más sencillo. Basta con echar una ojeada al diagrama para ver lo estrecha que es la "senda" de las negras en la octava fila. En ésta no disponen de escaques adyacentes al camino más corto y, por consiguiente, en este tramo del camino no se hallan en situación de soportar la menor desviación, cosa que, por el contrario, pueden permitirse las blancas.

La solución debe estar ya clara: 1.Rf3 Rg5 las negras se ven obligadas a realizar una marcha "paralela" 2.Re2 Rf6 3.Rd3 Re7 4.Rc3! [El blanco ha comenzado la maniobra decisiva (utilización del "triángulo") en la cuarta jugada. El aplazarla hubiese sido, para la estructura de los peones que se considera erróneo; por ejemplo: 4.Rc4 Rd8 5.Rb4?! (Más fuerte es 5.Rd3! Re7 6.Rc3!+- ganando. Este es un ejemplo de posición "reversible"; si las negras no se hallasen tan privadas de movimientos, es decir, si dispusieran de una zona suficiente en la retaguardia, semejante equivocación podría llevar a tablas, y no debe perderse de vista que estas posiciones "reversibles" aparecen con bastante frecuencia.) 5...Rc8 y las negras tienen opciones de defensa, aunque su esperanza se pierde luego de 6.Rc4 Rb8 con lo que se ponen en condiciones de atacar a los peones e3 y e4 7.Rd3 Ra7 8.Re2 Rb6 9.Rf3 Rc5 10.Rg4 Rc4 11.Rxh4 Rd3 12.Rg4 Rxe4 13.h4 Rxe3 14.h5 e4 15.h6 Rd3 16.h7 e3 17.h8D e2 18.Da1+- y el blanco gana] 4...Re8 las negras han podido todavía contestar a la desviación del rey blanco, pero ya no pueden repeler la segunda y siguiente desviación 5.Rb4! Rd8 6.Rc4! y ganan 6...Rc8 [o también si 6...Re7 entonces 7.Rb5 ganando] 7.Rd3+- Esta posición de análisis es muy sencilla, el tipo de maniobra que ésta no hubiera variado aun siendo otra la posición de los reyes.