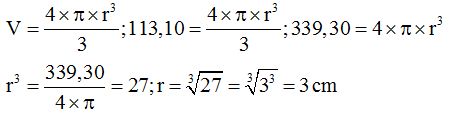Cuerpos Geométricos Redondos: Volúmen del Tronco del Cono - Esféricas - Volúmen de la Esfera
Podemos calcular:
a) Hallamos el volumen total del cono y le restamos el volumen del cono deficiente o la parte del cono que ha sido cortada por el plano (como ves, repetimos los referido a la pirámide).
Aplicando al cono de la última figura tenemos:
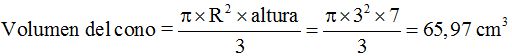
A este valor le descontamos el valor del volumen del tronco deficiente:
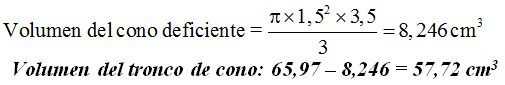
b) Existe una fórmula que por las complicaciones de su deducción la omitimos. Esta fórmula utilizada desde hace siglos es:
R representa el radio de la base.
r es el radio del círculo formado por la intersección del plano con el cono.
h es la altura del tronco de cono.
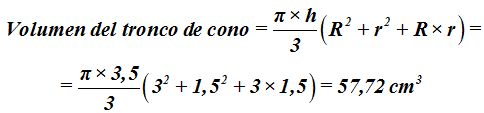
Los resultados son iguales. Utiliza la que prefieras.
15(3).35 Calcula el volumen del tronco de cono cuyas medidas en centímetros los tienes en la figura siguiente. Utiliza el procedimiento que quieras:
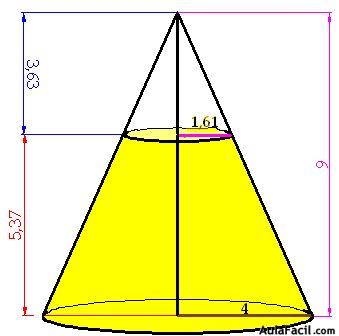
Respuesta: 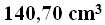
ESFERA.
La palabra esfera procede de la palabra griega sfaira que significa pelota.
La esfera es un cuerpo geométrico limitado por una superficie curva cuyos puntos están a igual distancia (equidistan) de otro punto que está en el interior de esta superficie al que llamamos centro.
A la distancia que hay desde un punto cualquiera de la superficie esférica al centro llamamos radio de la esfera.
Al referirte a la esfera piensa que es el espacio hueco que hay dentro de la superficie curva.
En la figura siguiente tenemos una esfera en la que indicamos con la palabra radio la distancia de cualquier punto de la superficie esférica al centro:
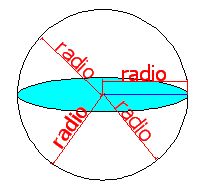
VOLUMEN DE LA ESFERA.
Arquímedes, griego (250 años antes de CRISTO) uno de los más grandes matemáticos de la historia descubrió un modo muy interesante para calcular el volumen de una esfera.
Para ello, se sirvió de una semiesfera (mitad de la esfera), un cono y un cilindro.
Los tres cuerpos geométricos deben tener las mismas medidas en cuanto al radio y la altura.
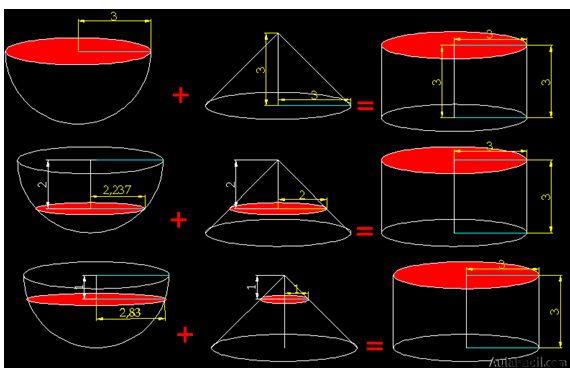
En la figura ves una semiesfera de 3 cm. de radio, un cono de 3 cm. de radio y 3 cm. de altura y un cilindro de 3 cm. de altura y 3 cm. de radio.
Analizamos cada línea de la figura:
En la 1ª línea de la figura damos un corte con un plano paralelo a 3 cm. de la base.
Lógicamente este corte ha producido una sección (color rojo) en la esfera que corresponde a un círculo de 3 cm. de radio.
En el cono no ha producido sección ninguna porque el corte lo hemos dado a 3 cm. de la base y corresponde a al punto del vértice.
En el cilindro el corte nos ha producido un círculo también de 3 cm. de radio.
Si calculamos las áreas de las secciones producidas por el corte de los cuerpos geométricos con el plano horizontal obtenemos:

Observa que la suma de las áreas de las secciones de la semiesfera y cono tiene el mismo valor que la sección del cilindro.
En la 2ª línea de la figura damos un corte con un plano paralelo a 1 cm. de la base.
Lógicamente este corte ha producido una sección (color rojo) en la esfera que corresponde a un círculo de 2,237 cm. de radio.
En el cono el círculo tiene un radio de 2 cm.
En el cilindro mantiene su radio de 3 cm.

La suma de las áreas de las secciones de la semiesfera y cono tiene el mismo valor que la sección del cilindro.
En la 3ª línea de la figura damos un corte con un plano paralelo a 2 cm. de la base.
Lógicamente este corte ha producido una sección (color rojo) en la esfera que corresponde a un círculo de 2,83 cm. de radio.
En el cono ahora el radio vale 1 m.
El valor del radio del cilindro se mantiene el mismo.

De este modo, Arquímedes nos dice que cuantas secciones realicemos siempre se producirá que la suma de las áreas de las secciones de la semiesfera y cono será igual al área de la sección del cilindro.
Si sumamos los volúmenes de la semiesfera y cono veremos que la suma coincide con el volumen del cilindro siempre que las medidas del radio y alturas son iguales en los tres cuerpos geométricos.
Fíjate que bien que las alturas del cono y cilindro son iguales a los radios.
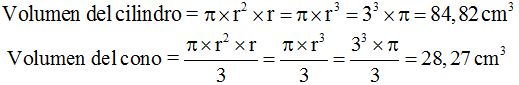
Como el volumen de la semiesfera + volumen del cono = volumen del cilindro según los datos anteriores, el volumen de la semiesfera será igual: volumen del cilindro – volumen del cono.
Volumen de la Semiesfera = Volumen del Cilindro - Volumen del Cono
es decir,

Hemos llegado a obtener la fórmula de la semiesfera
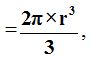
luego, para saber la fórmula de la esfera tendremos que multiplicar por 2 a
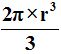 ,
,
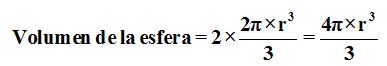
15(3).36 Calcula el volumen de una esfera de 5 cm., de radio.
Respuesta: 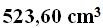
16(3).37 Una esfera de 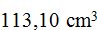 de volumen ¿Cuánto vale su radio?
de volumen ¿Cuánto vale su radio?
Respuesta: 3 cm.
Solución: