Barra de Menú Principal: Analizar (II)
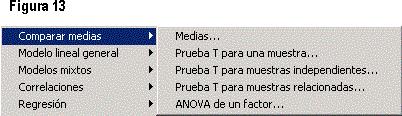
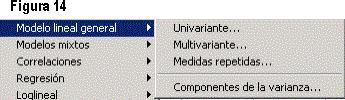
La figura 14 presenta la opción de Modelo lineal general, que incluye los siguientes apartados: Univariante (proporciona un análisis de regresión y un análisis de varianza para una variable dependiente mediante uno o más factores o variables); Multivariante (proporciona un análisis de regresión y un análisis de varianza para variables dependientes múltiples por una o más covariables o variables de factor); Medidas repetidas (analiza grupos de variables dependientes relacionadas que representan diferentes medidas del mismo atributo); Componentes de la varianza (se emplea para modelos de efectos mixtos, estima la contribución de cada efecto aleatorio a la varianza de la variable dependiente).
Posterior al Modelo lineal general, los siguientes apartados son: Modelos mixtos (en este cuadro de diálogo le facilita al investigador seleccionar variables que definen sujetos y observaciones repetidas, y elegir una estructura de covarianzas para los residuos) y Correlaciones (incluye correlaciones parciales, bivariadas y distancias).
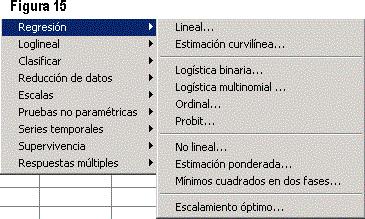
La figura 15 presenta la subopción de Regresión, que incluye los siguientes apartados: Lineal (estima los coeficientes de un modelo lineal, con una o más variables independientes, que mejor prediga el valor de la variable dependiente); Estimación curvilínea (genera estadísticos de estimación curvilínea por regresión y gráficos relacionados para varios modelos diferentes de estimación curvilínea por regresión); Logística binaria (es de mucha utilidad para los casos en los que se desea predecir la presencia o ausencia de una característica o resultado según los valores de un conjunto de variables predictoras); Logística multinomial (es útil en aquellas situaciones en las que el investigador desee poder clasificar a los sujetos según los valores de un conjunto de variables predictoras); Ordinal (permite dar forma a la dependencia de una respuesta ordinal politómica sobre un conjunto de predictores, que pueden ser factores o covariables); Probit (mide la relación entre la intensidad de un estímulo y la proporción de casos que presentan una cierta respuesta a dicho estímulo); No lineal (es un método para encontrar un modelo no lineal para la relación entre la variable dependiente y un conjunto de variables independientes); Estimación ponderada (permite calcular los coeficientes de un modelo de regresión lineal mediante mínimos cuadrados ponderados -MCP, WLS-, de forma que se les dé mayor ponderación a las observaciones más precisas -es decir, aquéllas con menos variabilidad- al determinar los coeficientes de regresión); Mínimos cuadrados en dos fases (utiliza variables instrumentales que no estén correlacionadas con los términos de error para calcular los valores estimados de los predictores problemáticos); Escalamiento óptimo (amplía la aproximación típica mediante un escalamiento de las variables nominales, ordinales y numéricas simultáneamente).
Después de Regresión, tenemos la opción Loglineal analiza las frecuencias de las observaciones incluidas en cada categoría de la clasificación cruzada de una tabla de contingencia, e incluye los apartados de General, Logit y Selección del modelo .
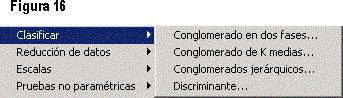
En la figura 16 se tiene la subopción de Clasificar, que es una de las subopciones que mayor uso tiene cuando de realizar análisis de conglomerados se trata. Cuenta con los siguientes ítems: Conglomerados en dos fases (es una herramienta de exploración que descubre las agrupaciones naturales -o conglomerados- de un conjunto de datos que, de otra manera, no sería posible detectar);Conglomerado de K medias (con este procedimiento se intenta identificar grupos de casos relativamente homogéneos basándose en las características seleccionadas y utilizando un algoritmo que puede gestionar un gran número de casos); Conglomerados jerárquicos (combina los conglomerados basándose en las características seleccionadas y los clasifica en orden de jerarquía); Discriminante (este análisis resulta útil para las situaciones en las que se desea construir un modelo predictivo para pronosticar el grupo de pertenencia de un caso a partir de las características observadas de cada uno de ellos).