Conceptos: Cóncavo y Convexo
Los conceptos de cóncavo y convexo, a veces, se nos olvidan y otras veces, no estamos seguros cuando hablamos de una línea cóncava o convexa.
Cuando contemplamos la línea de la circunferencia desde el interior de la misma nos referimos a una curva cóncava, lo que vemos desde el exterior es una curva convexa.
Mickey el ratón, desde el exterior examina a una parábola convexa.
Desde el interior contempla una parábola cóncava.
Si las ramas de la parábola están hacia abajo, la parábola sigue siendo cóncava:

El conejo lo sabe muy bien. Para el león es convexa. Según el punto de vista del observador la misma línea puede ser cóncava o convexa.
Si la cosa no te ha quedado clara observa un chichón en tu frente, lo notas, lo palpas, lo ves situado frente al espejo, eso es convexo.
Si tu papá o mamá se ha comprado un coche y el día del estreno se da un golpe, la chapa de la carrocería se ha introducido y la curva será cóncava. Se lo dices, a lo mejor le alivias su estado emocional.
En las parábolas con ramas hacia arriba, el valor de a siempre vale más que 0.
Las parábolas con ramas hacia abajo el valor de a siempre vale menos que 0, es decir, el valor de a es negativo.
Las parábolas 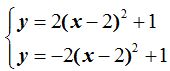 que ves en la figura siguiente tienen sus vértices en el mismo punto (2,1).
que ves en la figura siguiente tienen sus vértices en el mismo punto (2,1).
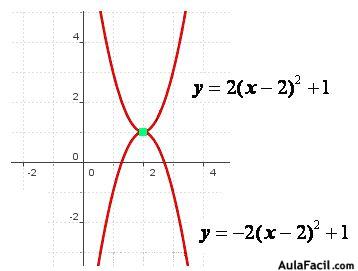
El mínimo valor que adquiere y en la primera función equivale al máximo valor de yen la segunda.
Es importante que te fijes en el valor de la abscisa, es decir, de x. Este valor no varía aunque cambie el valor de a.
13.92 Comprueba que las coordenadas del vértice de:
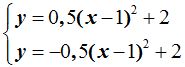
son las mismas para las dos parábolas
¿Cuál es ese punto?
Respuesta: (1,2)
CALCULAR LAS COORDENADAS DEL VÉRTICE DE UNA PARÁBOLA ENUNCIADA EN LA FORMA GENERAL:
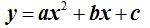
Este problema se reduce a calcular el valor de x, es decir, el de la abscisa y después sustituirlo en la ecuación para determinar el valor de y.
En todos los ejercicios que hemos realizado con funciones del tipo: 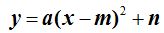
habrás comprobado que el vértice se encuentra en el punto (m,n).
Ejemplos:

¿Cómo pasamos de 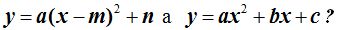
Es muy importante que recuerdes que el valor de n no altera el valor de la abscisa x en el vértice. El valor de x sigue siendo el mismo tenga n cualquier valor. El valor de n hace que la parábola se desplace verticalmente el vértice las unidades que señala esta variable, pero el valor de la abscisa sigue siendo el mismo, esto quiere decir que, las siguientes parábolas:
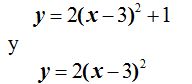
tienen el mismo valor de abscisa: (3,1) y (3,0). La diferencia radica en que el vértice se ha desplazado una unidad respecto al eje y.
Tenemos 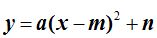 y la forma general
y la forma general 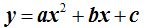 Haciendo operaciones en
Haciendo operaciones en 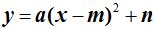 tenemos en :
tenemos en :
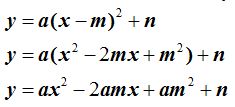
Comparamos 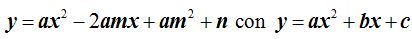 y vemos que:
y vemos que:
1.-Las dos expresiones contienen el mismo término: 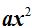
2.-Los términos que no contienen a x son términos independientes.
Podemos decir que 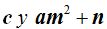 son términos independientes que tienen el mismo valor.
son términos independientes que tienen el mismo valor.
3.- Luego, 2amx y bx tendrán que ser iguales:
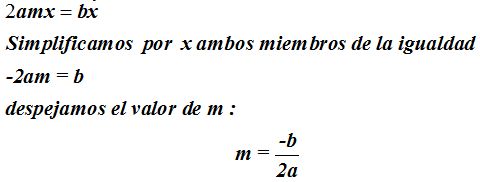
4.- Si 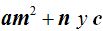 son iguales podemos decir que:
son iguales podemos decir que:

Conocidos los valores de m y n ya podemos saber las coordenadas del vértice de una parábola a partir de la ecuación de 2º grado: 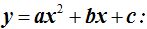
Ejemplo:
Hallar el vértice de la parábola: 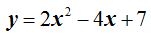
El valor de la abscisa en el vértice será: 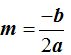 donde sustituyendo los valores conocidos tendremos:
donde sustituyendo los valores conocidos tendremos: 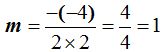
Para calcular el valor de la ordenada del vértice podemos hacer dos cosas:
1ª Sustituir el valor que acabamos de hallar en 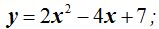
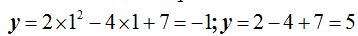 con lo que sabemos que el vértice de la parábola se encuentra en el vértice (1,5).
con lo que sabemos que el vértice de la parábola se encuentra en el vértice (1,5).
2ª Utilizar la fórmula 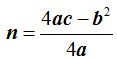
Sustituyendo por los valores que conocemos tendremos:
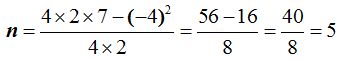
Como ves, obtenemos el mismo resultado del valor de la ordenada del vértice que en la forma anterior.
Elige el que te sea más sencillo.
13.93 Calcula las coordenadas del vértice de la función cuadrática: 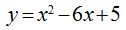
Respuesta: el punto (3,-4)
13.94 ¿Cuáles son las coordenadas del vértice de la función 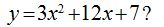
Respuesta: el punto (-2,-5)
13.95 ¿Cuáles son las coordenadas del vértice de la función 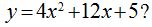
Respuesta: el punto (-1.5,-4)

