Interpolación de Medios Geométricos
Se trata de calcular la razón para que los términos a interpolar entre dos números dados formen una progresión geométrica.
Cuanto se dijo en la interpolación de medios aritméticos es válido, únicamente debes tener en cuenta que de la fórmula del último término de una progresión geométrica, despejamos la razón y el número de términos será igual a los dos que nos dan: primero y último más el número de los medios geométricos, total n+2 términos:
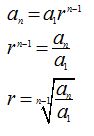
16.18 Calcula la razón para interpolar entre 11 y 5632, ocho medios geométricos, y después, escribe la progresión.
Respuesta: r = 2;la progresión es = 11: 22: 44: 88: 176: 352: 704: 1408: 2816: 5632
Solución:
Aplicas la fórmula y sustituyes las letras por sus valores
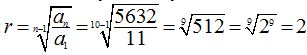
16.19 En la progresión geométrica: 3: 6: 12:…………el producto de dos términos consecutivos es 1152. ¿Cuáles son estos términos?
Respuesta: 4º y 5º términos.
Solución:
Sea x el primero de los términos que nos piden. El segundo será: 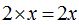
El producto de los valores de estos dos términos es: 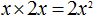
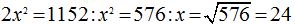
Si el tercer término vale 12 y la razón 2, el cuarto será: 12 x 2 = 24.
El 5º término valdrá 48.
16.20 La suma de dos términos consecutivos de la progresión 6: 18: 54: …………. es 157464 . ¿Cuáles son estos términos?
Respuesta: 9º y 10º términos
Autor: Agradecemos a Don Ignacio Pujana el envío de éste magnífico curso.

