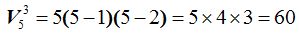Teoría Combinatoria
La Combinatoria es una rama de las matemáticas cuyo objeto es estudiar las posibles agrupaciones de objetos que podemos llevar a cabo de un modo rápido teniendo en cuenta las relaciones que deben existir entre ellas.
Por ejemplo:
Con 5 colores diferentes ¿cuántas banderas tricolores podemos hacer? Una bandera de otra se diferencia en tener un color diferente o en el orden de colocación de los colores.
Estas 3 banderas son diferentes y pertenecen a Luxemburgo, Rusia y Yugoslavia.
Si te dicen que con 5 colores diferentes podemos hacer 10 banderas tricolores probablemente dudarías un poco.
Con las cifras 1, 2, 3, 4, 5 y 6 ¿cuántos números de tres cifras, diferentes, por supuesto, puedo formar? Un número es diferente de otro si tiene una cifra distinta o el orden de sus cifras es diferente. 321 y 123 son números distintos aunque tengan las mismas cifras.
Con los datos anteriores podríamos formar 20 números diferentes.
¿De cuántas maneras diferentes pueden sentarse los 25 alumnos de la clase en los pupitres?
Si te dicen que de muchas, te quedas igual, pero si te dicen que de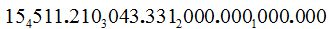 
maneras diferentes quizá no lo creas, sí, el número tiene 26 cifras. Parece imposible.
La Teoría Combinatoria es la parte de Matemáticas que se encarga de crear grupos de datos, objetos, etc., y además de llevar a cabo los cálculos necesarios.
Entre las diferentes formas que hay para llevar a cabo estos agrupamientos tenemos las:Variaciones, Permutaciones y Combinaciones.
¿A qué se llama factorial de un número?
Factorial de un número es el producto de todos los factores decrecientes a partir de él hasta llegar a la unidad.
El factorial de un número se escribe k! (siendo k cualquier número entero positivo)
Ejemplo:
Factorial de 3, se escribe 3! y se lee factorial de tres y no, tres factorial.
El valor de 3! es el producto de los factores decrecientes a partir de 3 hasta llegar a 1:
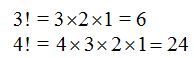
18.1 ¿Cuánto vale el factorial de 5?
Respuesta: 120
VARIACIONES SIN REPETICIÓN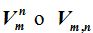 
Llamamos variaciones a los distintos grupos de elementos que podemos formar tomados de n en n de un total de m elementos.
Ejemplo:
¿Cuántos grupos de 2 cifras (n) podemos formar con las tres primeras cifras (m)?
Sirviendo de un diagrama de árbol podemos hacer:
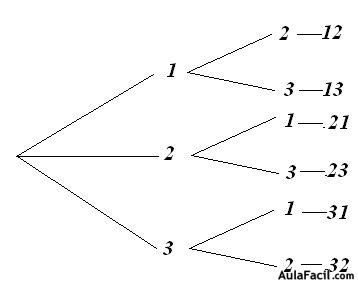
Los grupos de 2 elementos son: 12, 13, 21, 23, 31 y 32
Vemos que con 3 cifras podemos formar 6 números diferentes de dos.
Con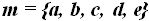 
tomados de 3 en 3, es decir, 
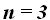¿cuántos grupos diferentes o variaciones puedo hacer?
Compruebo que puedo hacer 60 variaciones.
Dirás con toda razón que hacer un trabajo de éstos lleva mucho tiempo y que siempre estás corriendo el riesgo de cometer equivocaciones. Tienes razón, lo que sucede es que casi nunca nos interesa ver los grupos que se pueden formar sino cuántos se pueden hacer.
Por simple observación comprobamos en el primer ejemplo que con 3 elementos tomados de 2 en 2 hemos formado 6 grupos. Es decir, con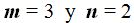 
hemos obtenido 6 variaciones.
Si al valor de m multiplicas por el siguiente valor inferior a él (3) en una unidad (m-1) que es (n)2, y el número de factores es igual al valor de n (dos factores) las Variaciones de 3 elementos tomados de dos en dos es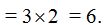 
Esto se escribe:
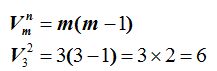
También podemos escribir:
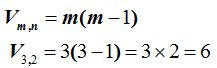
18.2 Con las cifras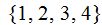 
¿cuántos números de 3 cifras puedo formar?
Respuesta: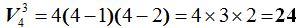 
números diferentes.
Solución: m=4 y n=3
A partir de 4 (m) tomo tres (n) factores decrecientes de unidad en unidad a partir de 4.
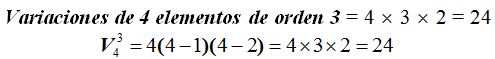
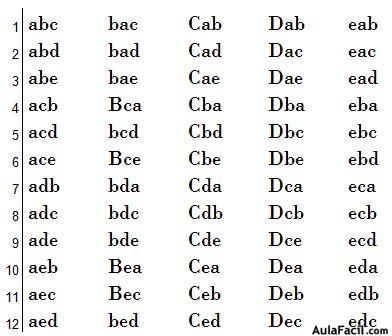
18.3 Con las 5 (m) primeras letras del alfabeto ¿cuántas palabras de 3(n) letras puedo formar?
Respuesta: 60
Solución
El valor de m=5
El valor de n=3
