Simplificación de Fracciones
Simplificar significa hacer más sencillo, reducir a una forma más sencilla.
Para simplificar los números o términos deben estar multiplicando. ¡ Cuidado! Si los números o términos están sumando o restando no se deben simplificar .
La operación para simplificar es la división. Se divide al numerador y denominador por el factor común más grande.
Ejemplo:
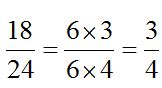
Podríamos haber simplificado por 2, pero habríamos comprobado que todavía podíamos simplificarlo por 3.
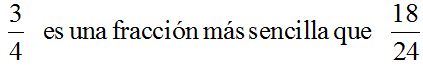
Simplificar expresiones algebraicas es muy sencillo. Te basta con recordar que potencias de la misma base, se restan los exponentes y el resultado se coloca allí donde el exponente era mayor.
Simplificar expresiones algebraicas es muy sencillo. Te basta con recordar que potencias de la misma base, se restan los exponentes y el resultado se coloca allí donde el exponente era mayor.
9.97 Simplifica: 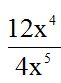
Respuesta:
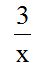
Solución: La parte numérica del numerador y del denominador la dividimos por 4. La parte literal está formada por potencias de la misma base, por lo tanto, restamos sus exponentes. El resultado lo colocamos allí donde el exponente era mayor:
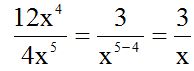
9.98 Simplifica las fracciones siguientes:
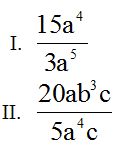
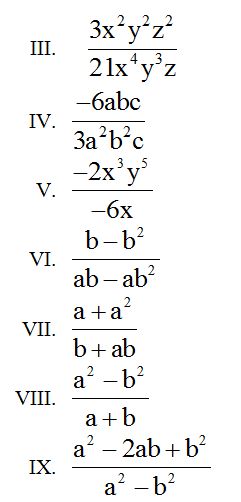
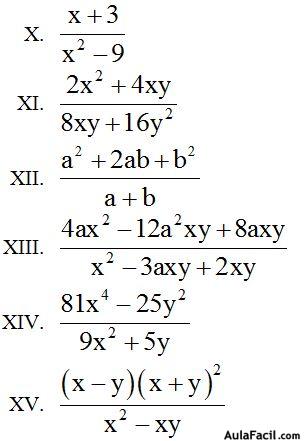
Respuestas:
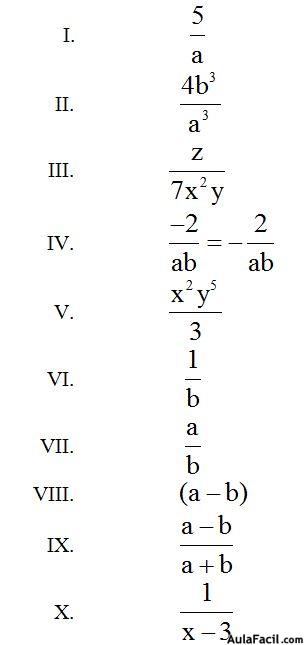
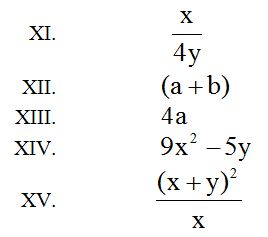
Soluciones:
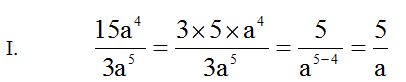
Recuerda lo que hemos dicho anteriormente:
a) la parte numérica se simplifica separadamente de la literal.
b) Para dividir potencias de la misma base se restan los exponentes y el resultado se coloca en el lugar donde el exponente era mayor. En el caso que nos ocupa, como a5 es mayor que a4 lo escribiremos en el denominador:
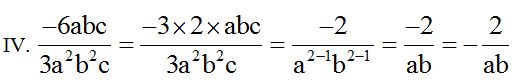
Cuando los valores del numerador y denominador son iguales los anulamos. En este caso la letra ‘c’.
Cuando los signos del numerador y denominador son diferentes, el resultado es negativo.
Es lo mismo escribir: 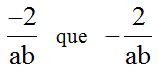 porque el signo
porque el signo 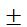 por delante de una fracción le afecta solamente al numerador.
por delante de una fracción le afecta solamente al numerador.
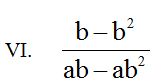
Cuando los términos están sumando o restando no se deben simplificar, han de estar multiplicando.
En el numerador podemos sacar a ‘b’ como factor común y en el denominador a ‘ab’:
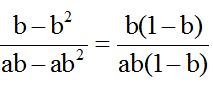
Ahora ya hemos transformado al numerador y denominador en un producto. Dado que el factor 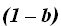 ) lo tenemos en el numerador y denominador, lo tachamos de ambos lugares ya que
) lo tenemos en el numerador y denominador, lo tachamos de ambos lugares ya que 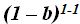 es igual a
es igual a 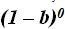 y como una potencia de exponente cero es igual a 1, cualquier número por 1 no cambia su valor.
y como una potencia de exponente cero es igual a 1, cualquier número por 1 no cambia su valor.
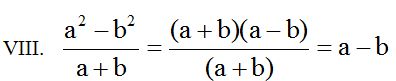
Como el numerador procede de la suma de dos números por su diferencia (a + b)(a – b) y en el denominador tenemos (a + b), los simplificamos suprimiéndolos y nos queda (a – b).
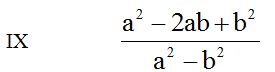
En el numerador tienes el desarrollo del cuadrado de la diferencia de dos números y debajo el resultado del producto de la suma de dos números por su diferencia:
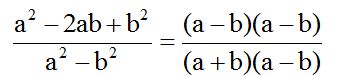
El factor (a – b) que lo tenemos en el numerador y denominador lo podemos simplificar (eliminar) y nos queda:
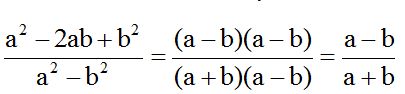

El denominador es una diferencia de cuadrados porque 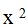 y 9 son cuadrados. Una diferencia de cuadrados procede de la suma de dos números por su diferencia (x + 3)(x – 3):
y 9 son cuadrados. Una diferencia de cuadrados procede de la suma de dos números por su diferencia (x + 3)(x – 3):
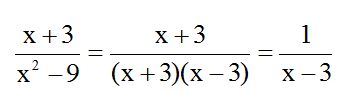
En el numerador podemos sacar factor común a ‘2x’ que al dividir cada término entre este valor nos queda dentro del paréntesis: (x + 2y). En el denominador sacamos factor común a ‘8y’ y el cociente de dividir cada término entre este valor lo colocamos dentro del paréntesis:
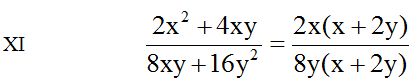
Simplifico al numerador y denominador por (x + 2y) y me queda:
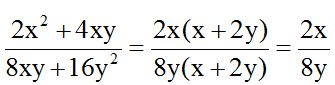
Al numerador y denominador les puedo dividir por 2:
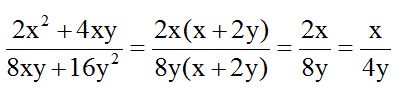
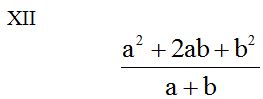
El numerador es el desarrollo del cuadrado de la suma de dos números: 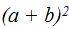 que es lo mismo que (a + b)(a + b):
que es lo mismo que (a + b)(a + b):
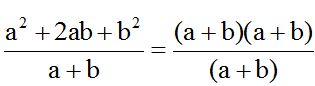
No tengo más que simplificar al numerador y denominador por (a + b):
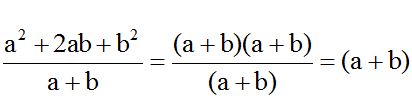
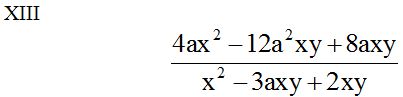
En este ejercicio saco factor común en el numerador a ‘4a’ y al dividir cada término por este valor obtengo:
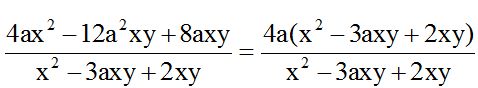
que como habrás observado, son los mismos valores que hay en el denominador. Al denominador le puedes considerar como un factor si le encierras en un paréntesis.
Simplificamos lo que tienes entre paréntesis y nos queda:
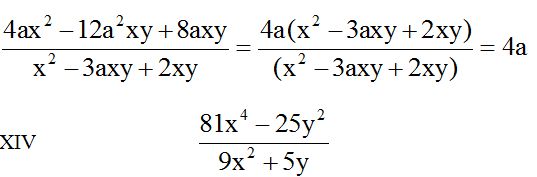
En este ejercicio ves que el numerador es una diferencia de cuadrados.

Después simplificamos los factores iguales:
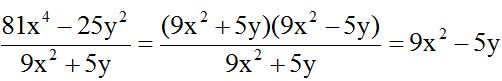
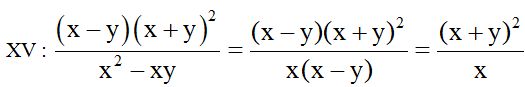
Basta sacar factor común a ‘x’ en el denominador para poder simplificar los factores iguales.

