Problema 23 Método Simplex

Una determinada empresa debe determinar para el próximo año un programa que conlleve el mínimo coste posible. Los dos productos que puede fabricar le hacen incurrir en un coste de 8 u.m./u.f. si se trata del producto Z y 10 u.m./u.f. si es el producto W. en cuanto al consumo de materias primas sólo existe restricción en cuanto al componente AB, del cual el producto Z consume 2 u.f. por unidad de producto y el W 1u.f. por unidad de producto, disponiéndose de 600 u.f. de dicho componente al mes.

Diferentes imposiciones legales establecen la obligación de producir al menos 100 u.f. de producto Z al mes y un mínimo de 350 u.f. entre los dos productos.¿Cuál será, en base a esta información el programa de producción para el próximo mes que lleva al mínimo coste?

SOLUCIÓN:

ZMIN = 8X1 + 10X2
2X1 + X2 ≤ 600
X1 ≥ 100
X1 + X2 ≥ 350
Xi ≥ 0

Introducimos las variables de holgura y las variables artificiales:

ZMIN= 8X1+ 10X2 + 0h1 + 0h2 + 0h3 + A1M + A2M
2X1 + X2+ h1 = 600
X1 – h2 + M = 0
X1 + X2 – h3 + M = 350
Xi ≥ 0; M ≥ 0

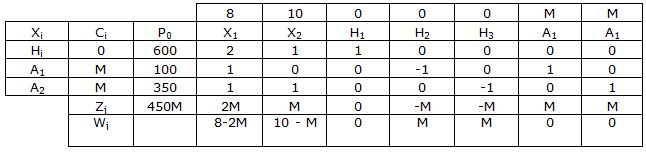
Entra X1 y sale A1:

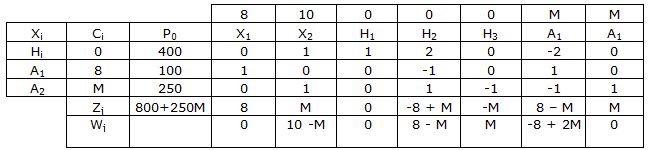
Entra h2 y sale h2:

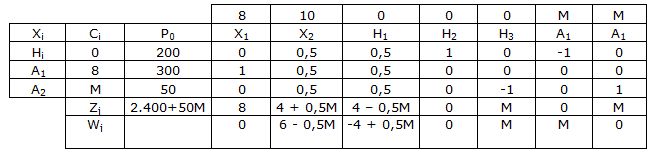
Entra X2 y sale A2:

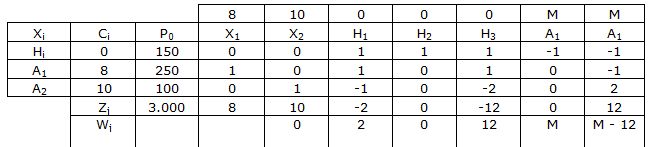
Y una vez llegado hasta aquí, observamos que los rendimientos son mayores o iguales a 0 y estamos minimizando, lo cual hemos alcanzado el óptimo, donde se fabricarán:

X1 = 8 unidades del producto Z
X= 10 unidades del producto W.
Coste = 3.00 u.m