Desarrollo sobre el papel de un prisma recto
Para hacer el desarrollo de una prisma recto sobre una hoja de papel, tenemos primero que observar la perspectiva y las vistas principales realizadas anteriormente, para así, poder decidir en cuantas partes lo vamos a descomponer, debiendo procurar que sean las menos posibles.
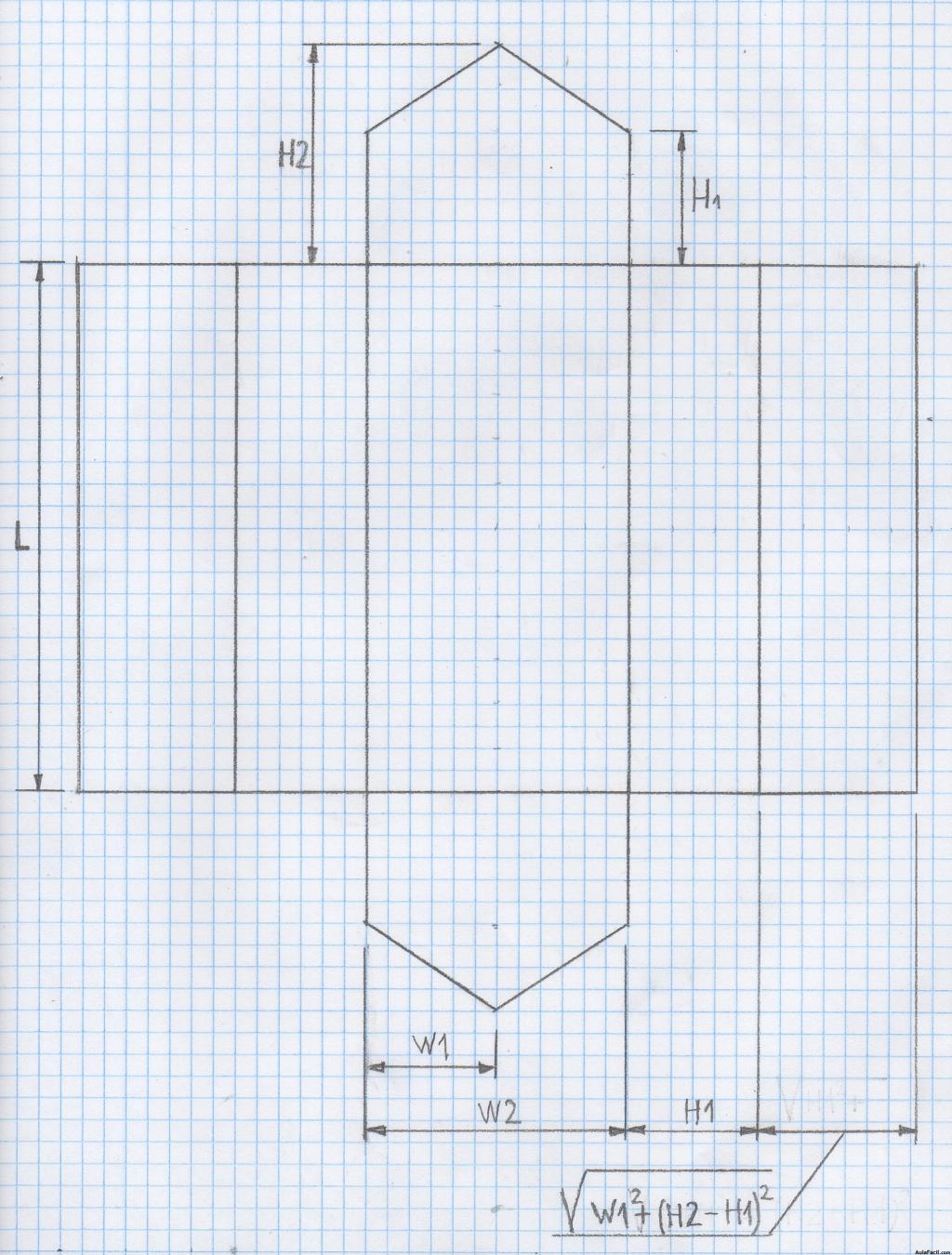
Figura 31
En este caso vemos que podemos descomponerlo en una plantilla de siete partes: dos pentágonos irregulares iguales pero simétricos que se corresponderán con las superficies frontal y posterior, dos rectángulos iguales que serán las superficies inclinadas superiores, otros dos rectángulos iguales que serán las superficie verticales laterales y un rectángulo que será la superficie horizontal de la base. Un ejemplo muy claro de este objeto, sería una casa con el tejado a dos aguas.
Estas siete partes serán, en el papel, superficies planas donde los lados verticales de los rectángulos deberán tener todos la misma longitud, los lados horizontales de los rectángulos de los extremos deberán tener la misma longitud que los lados inclinados de los pentágonos y por último los lados horizontales de los rectángulos intermedios deberán ser iguales que los lados verticales de los pentágonos
Estas igualdades se deben a que éstas superficies comparten aristas y por tanto sus longitudes deben ser idénticas para que después puedan coincidir exactamente a la hora de plegar el papel y unir las partes con el adhesivo.
A la vista de las figuras 29, 30 y 31, tendremos que tener en cuenta las siguientes fórmulas matemáticas:
1ª) La longitud de los lados inclinados de los pentágonos que forman las superficies frontal y posterior tendremos que calcularla o medirla directamente en las vistas frontales A ó B. En caso de que la calculemos, vendrá dada por las proyecciones horizontal y vertical de estos lados que se corresponderán con la cota horizontal W1 y la diferencia de alturas H2 – H1 respectivamente. Aplicaremos el teorema de Pitágoras que nos dice que la hipotenusa de un triángulo rectángulo h es igual a la raíz cuadrada de la suma de los cuadrados de los catetos, o lo que es lo mismo, la suma de los cuadrados de los catetos elevado a 1/2. En este caso los catetos serán W1 y H2-H1 por tanto :
h = (W12 + (H2-H1)2)1/2
sustituyendo las variables W1, H2 y H1 por 6, 10 y 6 cuadrículas respectivamente tendremos:
h = (62 + (10-6)2)1/2 = 7,21 cuadrículas, es decir 7 cuadrículas y cuarto aproximadamente.
Una vez conocidas las dimensiones W1, W2, H1, H2 y L y calculada h, podremos trazar las plantillas de un prisma recto.


