Regresión Múltiple. Resultados
Variables introducidas/eliminadas(b)
Modelo | Variables introducidas | Variables eliminadas | Método |
1 | Estatura del padre, Edad(a) | . | Introducir |
a) Todas las variables solicitadas introducidas
b) Variable dependiente: Estatura
La tabla anterior nos manifiesta que las “variables introducidas en el modelo han sido: la estatura del padre y la edad del joven, que no se tienen variables eliminadas, el método elegido ha sido el de “introducir”, y además nos dice que la variable dependiente es la “Estatura”.
Resumen del modelo(b)
Modelo | R | R cuadrado | R cuadrado corregida | Error típ. de la estimación |
1 | ,994(a) | ,988 | ,987 | 3,03763 |
a) Variables predictoras: (Constante), Estatura del padre, Edad.
b) Variable dependiente: Estatura
El modelo de regresión múltiple presenta un nivel de ajuste casi excelente, ya que la R tiene un valor de 0,994, en tanto que la R2 muestra un valor de 0,988 y la R2 corregida o ajustada tiene un valor de 0.987.
Coeficientes(a)
Modelo |
| Coeficientes no estandarizados | Coeficientes estandarizados | t | Sig. | |
|
| B | Error típ. | Beta |
|
|
1 | (Constante) | ,846 | 59,948 |
| ,014 | ,989 |
| Edad | 5,135 | ,284 | ,934 | 18,093 | ,000 |
| Estatura del padre | ,461 | ,326 | ,073 | 1,412 | ,181 |
a) Variable dependiente: Estatura
El modelo puede representarse de la siguiente forma:
Estatura = 5,135(edad) + 0,461(estatura del padre) + 0,846.
Puede explicarse el modelo de regresión múltiple así: “La estatura del niño o adolescente, es influenciada en 5,135 por cada año de edad que posea, más 0,461 por cada centímetro de estatura que tenga su padre, más una constante de 0,846”.
Recordemos la delimitación del modelo:
- Deben ser jóvenes entre 2 y 17 años.
- Para proyecciones, puede utilizarse uno o dos años de diferencia como máximo, ya sea con el límite inferior o el límite superior.
- Se ha considerado como un modelo lineal o de línea recta.
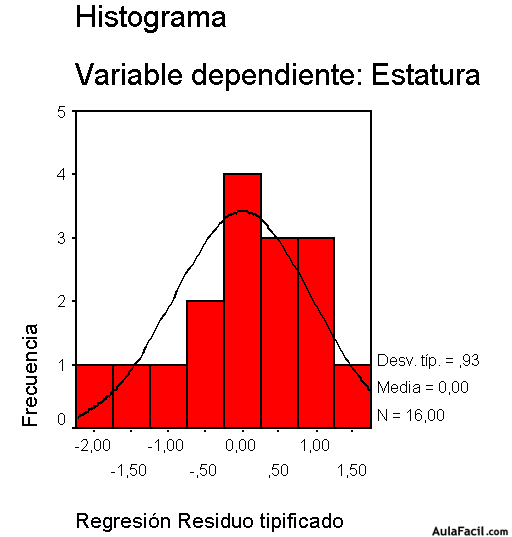
Este gráfico nos presenta la distribución bajo la curva normal de los residuos tipificados. Tiene una desviación típica de 0,93, y toma como variable dependiente a la “Estatura”.
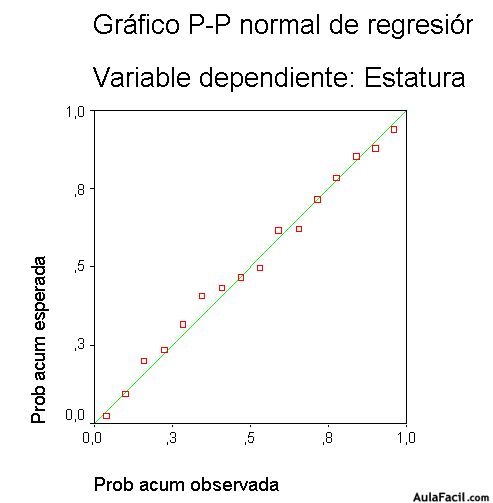
Este gráfico es bastante sugestivo. En el eje de las X tenemos la probabilidad acumulada observada, y en el eje de las Y tenemos a la probabilidad acumulada esperada. Como se puede ver a simple vista, la mayoría de puntos se encuentran sobre o muy cercanos a la recta, denotándose con ello un modelo que representa casi perfectamente a la realidad del fenómeno investigado.
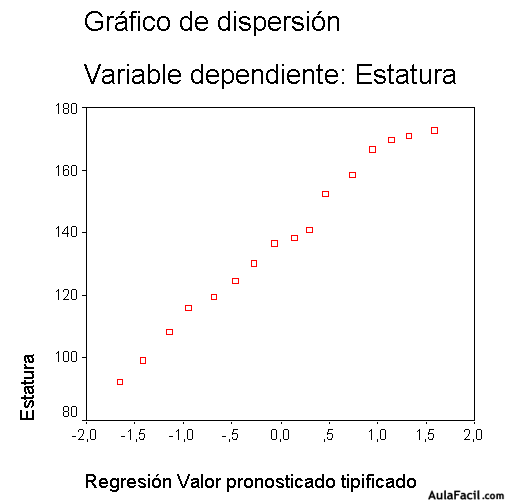
Este gráfico de dispersión presenta la “regresión del valor pronosticado tipificado” contra la “Estatura, y se observa claramente una relación positiva, ya que a medida se avanza en el cuadrante, los valores se incrementan.
Hasta acá llegamos con el Análisis de Regresión Múltiple, espero que estos ejemplos hayan sido de su satisfacción y le hayan mostrado el camino a seguir para realizar un análisis de éste tipo. Ahora nuestra atención se centrará en un modelo bastante interesante, el de Análisis de Correspondencias.
