Análisis de Conglomerados No Jerárquicos. Aplicación práctica (V).
Análisis de conglomerados de K medias
Centros iniciales de los conglomerados
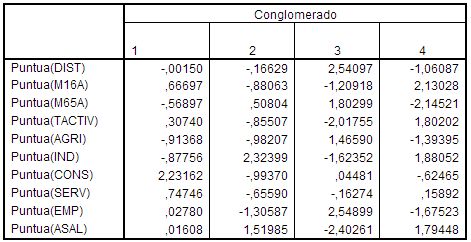
En este procedimiento, el historial de iteraciones se limita a registrar los distintos cambios producidos entre los centros de los grupos:
Historial de iteraciones(a)
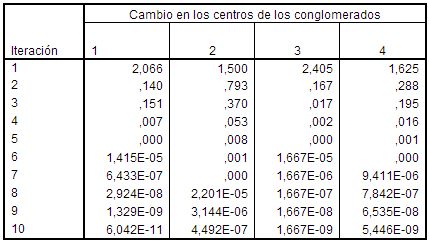
a) Se han detenido las iteraciones debido a que se ha alcanzado el número máximo de iteraciones. Las iteraciones no han logrado la convergencia. El cambio máximo de coordenadas absolutas para cualquier centro es de 2,246E-07. La iteración actual es 10. La distancia mínima entre los centros iniciales es de 5,034.
Naturalmente, no se ha producido la convergencia del procedimiento debido a que la exigencia que habíamos impuesto es muy fuerte, en el sentido de que solo admitiremos que el algoritmo ha llegado al final cuando no se producen más cambios.
La clasificación individual de cada paso en el conjunto general de observaciones se almacena en una nueva variable, llamada qcl_1 (se puede comprobar su aparición en la hoja de datos), y su distancia al centro del conglomerado al que pertenece en otra nueva variable, llamada qcl_2. En el visor de resultados aparece la siguiente tabla:
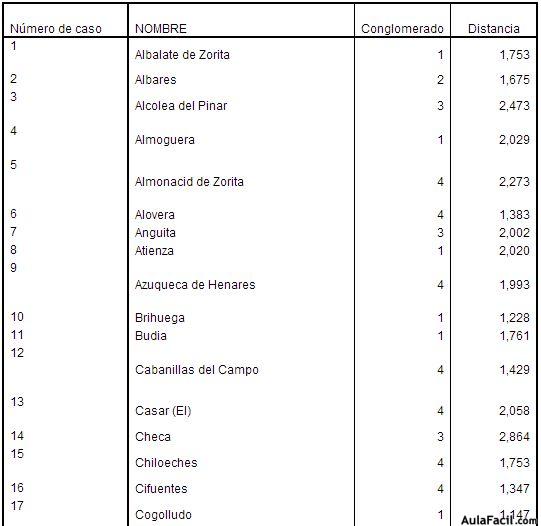
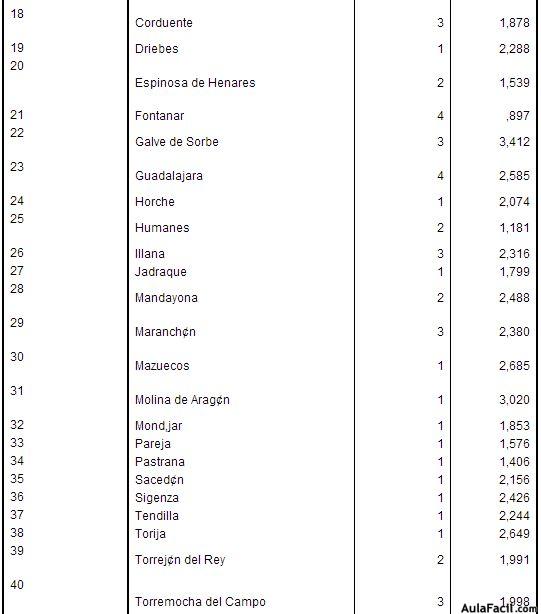

La matriz anterior nos muestra, caso por caso, el conglomerado de pertenencia de cada caso, así como la distancia existente del centroide con cada uno de los casos en cuestión.
Centros de los conglomerados finales
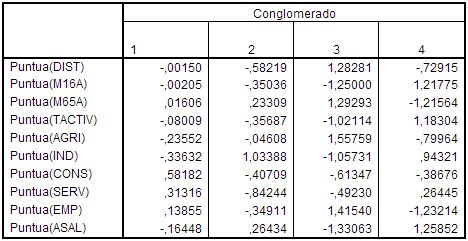
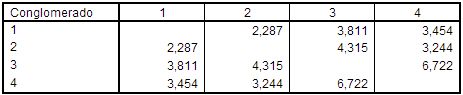
Por último, se presentan las distancias entre los centroides de los conglomerados resultantes:
Distancias entre los centros de los conglomerados finales
ANOVA
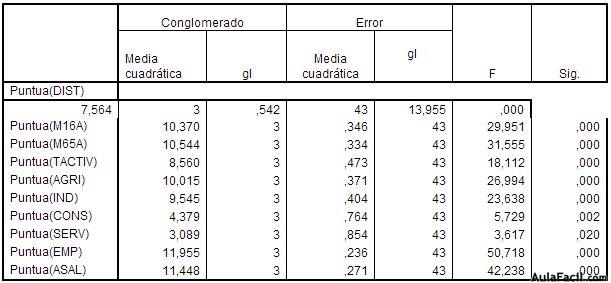
Las pruebas F sólo se deben utilizar con una finalidad descriptiva puesto que los conglomerados han sido elegidos para maximizar las diferencias entre los casos en diferentes conglomerados. Los niveles críticos no son corregidos, por lo que no pueden interpretarse como pruebas de la hipótesis de que los centros de los conglomerados son iguales.
Y se indica el número de casos que han resultado incluidos en cada conglomerado:
Número de casos en cada conglomerado

Finalmente, tenemos cuatro conglomerados resultantes, y el total de casos pertenecientes a cada conglomerado, además tenemos 47 casos válidos y ningún caso perdido. El conglomerado con mayor número de casos es el 1 con 21 y el conglomerado menor es el 2 con 6 casos. Si quisiéramos saber el orden o jerarquía de los conglomerados resultantes, tendríamos en este caso que aplicar una técnica de análisis de conglomerado jerárquico.
