Teorema Central del Límite: Ejercicios (I)

Ejercicio 1.

La renta media de los habitantes de un país se distribuye uniformemente entre 4,0 millones ptas. y 10,0 millones ptas. Calcular la probabilidad de que al seleccionar al azar a 100 personas la suma de sus rentas supere los 725 millones ptas.

Cada renta personal es una variable independiente que se distribuye según una función uniforme. Por ello, a la suma de las rentas de 100 personas se le puede aplicar el Teorema Central del Límite.

La media y varianza de cada variable individual es:

m = (4 + 10 ) / 2 = 7

s 2 = (10 - 4)^2 / 12 = 3

Por tanto, la suma de las 100 variables se distribuye según una normal cuya media y varianza son:

Media: n * m = 100 * 7 = 700

Varianza: n * s2 = 100 * 3 = 300

Para calcular la probabilidad de que la suma de las rentas sea superior a 725 millones ptas, comenzamos por calcular el valor equivalente de la variable normal tipificada:

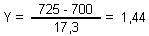
Luego:

P (X > 725) = P (Y > 1,44) = 1 - P (Y < 1,44) = 1 - 0,9251 = 0,0749

Es decir, la probabilidad de que la suma de las rentas de 100 personas seleccionadas al azar supere los 725 millones de pesetas es tan sólo del 7,49%

Ejercicio 2.

En una asignatura del colegio la probabilidad de que te saquen a la pizarra en cada clase es del 10%. A lo largo del año tienes 100 clases de esa asignatura. ¿Cuál es la probabilidad de tener que salir a la pizarra más de 15 veces?

Se vuelve a aplicar el Teorema Central del Límite.

Salir a la pizarra es una variable independiente que sigue el modelo de distribución de Bernouilli:

"Salir a la pizarra", le damos el valor 1 y tiene una probabilidad del 0,10

"No salir a la pizarra", le damos el valor 0 y tiene una probabilidad del 0,9

La media y la varianza de cada variable independientes es:

m = 0,10

s 2 = 0,10 * 0,90 = 0,09

Por tanto, la suma de las 100 variables se distribuye según una normal cuya media y varianza son:

Media: n * m = 100 * 0,10 = 10

Varianza: n * s2 = 100 * 0,09 = 9

Para calcular la probabilidad de salir a la pizarra más de 15 veces, calculamos el valor equivalente de la variable normal tipificada:

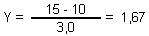
Luego:

P (X > 15) = P (Y > 1,67) = 1 - P (Y < 1,67) = 1 - 0,9525 = 0,0475

Es decir, la probabilidad de tener que salir más de 15 veces a la pizarra a lo largo del curso es tan sólo del 4,75% (¡¡¡ ánimo !!!, no es tan grave)