Distribuciones discretas: Poisson

Las distribución de Poisson parte de la distribución binomial:

Cuando en una distribución binomial se realiza el experimento un número "n" muy elevado de veces y la probabilidad de éxito "p" en cada ensayo es reducida, entonces se aplica el modelo de distribución de Poisson:

Se tiene que cumplir que:

" p " < 0,10

" p * n " < 10

La distribución de Poisson sigue el siguiente modelo:

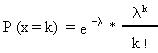
Vamos a explicarla:

El número "e" es 2,71828

" l " = n * p (es decir, el número de veces " n " que se realiza el experimento multiplicado por la probabilidad " p " de éxito en cada ensayo)

" k " es el número de éxito cuya probabilidad se está calculando

Veamos un ejemplo:

La probabilidad de tener un accidente de tráfico es de 0,02 cada vez que se viaja, si se realizan 300 viajes, ¿cual es la probabilidad de tener 3 accidentes?

Como la probabilidad " p " es menor que 0,1, y el producto " n * p " es menor que 10, entonces aplicamos el modelo de distribución de Poisson.

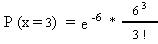
Luego,

P (x = 3) = 0,0892

Por lo tanto, la probabilidad de tener 3 accidentes de tráfico en 300 viajes es del 8,9%

Otro ejemplo:

La probabilidad de que un niño nazca pelirrojo es de 0,012. ¿Cuál es la probabilidad de que entre 800 recien nacidos haya 5 pelirrojos?

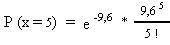
Luego,

P (x = 5) = 4,602

Por lo tanto, la probabilidad de que haya 5 pelirrojos entre 800 recien nacidos es del 4,6%.