Distribuciones discretas: Multihipergeométrica
La distribución multihipergeométrica es similar a la distribución hipergeométrica, con la diferencia de que en la urna, en lugar de haber únicamente bolas de dos colores, hay bolas de diferentes colores.
Ejemplo: en una urna hay 7 bolas blancas, 3 verdes y 4 amarillas: ¿cuál es la probabilidad de que al extraer 3 bolas sea cada una de un color distinto?
La distribución multihipergeométrica sigue el siguiente modelo:
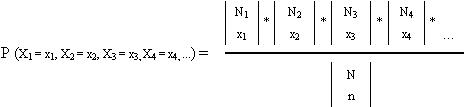
Donde:
X1 = x1: indica que el suceso X1 aparezca x1 veces (en el ejemplo, que una de las bolas sea blanca)
N1: indica el número de bolas blancas que hay en la urna (en el ejemplo, 7 bolas)
N: es el número total de bolas en la urna (en el ejemplo, 14 bolas)
n: es el número total de bolas que se extraen (en el ejemplo, 3 bolas)
Veamos el ejemplo:
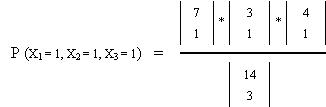
Luego:
P = 0,2307
Es decir, que la probabilidad de sacar una bola de cada color es del 23,07%.
Veamos otro ejemplo:
En una caja de lápices hay 10 de color amarillo, 3 de color azul y 4 de color rojo. Se extraen 7 lápices, ¿cual es la probabilidad de que 5 sean amarillos y 2 rojos?
Aplicamos el modelo:
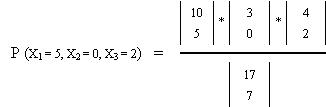
Luego
P = 0,0777
Por lo tanto, la probabilidad de que los 5 lápices sean de los colores indicados es del 7,77%.
