Resistencia de un conductor
Un conductor es un elemento pasivo que une los generadores con los receptores a través de los cuales circula la corriente.
Anteriormente se ha visto qué son las resistencias ideales/reales. Con los conductores ocurre lo mismo. A la hora de hacer los cálculos en un circuito como norma general no se considera resistencia alguna en los cables ni pistas del circuito.
Pero a la hora de hacer conexiones en baterías de coches, montar instalaciones eléctricas... la resistencia de los cables es algo que se debe tener en cuenta y ¡mucho! a la hora de calcular una instalación por la que circulará una intensidad elevada.
La resistencia de un conductor se calcula mediante la siguiente fórmula:
ρ= Coeficiente de resistividad del material (Suele venir en tablas) (En )
L= Longitud del cable (En m)
S= Sección del cable (En mm2)
Con la anterior fórmula se puede hallar la resistencia de un conductor, pero si éste se calienta por efecto del paso de la corriente (o cualquier otro estímulo), la resistencia variará y no circulará la corriente que deseamos por el circuito, o por lo menos no circulará la calculada. Esta variación se puede hallar mediante la siguiente fórmula:
ρf=ρ0*[1+α*(tf-t0)]
ρf= Coeficiente de resistividad final del material
ρ0= Coeficiente de resistividad inicial del material
tf= Temperatura final del material
t0= Temperatura inicial del material
α= Coeficiente de temperatura del material
(tf-t0) también se denomina incremento de temperatura o: (Δt)
De la anterior fórmula se puede obtener la variación de la resistencia así:
Rf=R0*[1+α*(tf-t0)]
y el coeficiente de temperatura para el cobre es: 3.93*10-3(ºC-1*10-3)
Estas dos fórmulas pueden parecer de poca importancia, pero se pueden obtener resultados y soluciones a problemas bastante interesantes, como veremos ahora:
- Se tiene un conductor de cobre de 200m de longitud y una sección de 1mm2 que alimenta una resistencia eléctrica de 500Ω. El cable está cortocircuitado con la fuente a 230V. Calcular la resistencia del cable(RL), la intensidad que circula por el circuito, la potencia perdida en el cable, la potencia en la resistencia y el rendimiento del circuito.
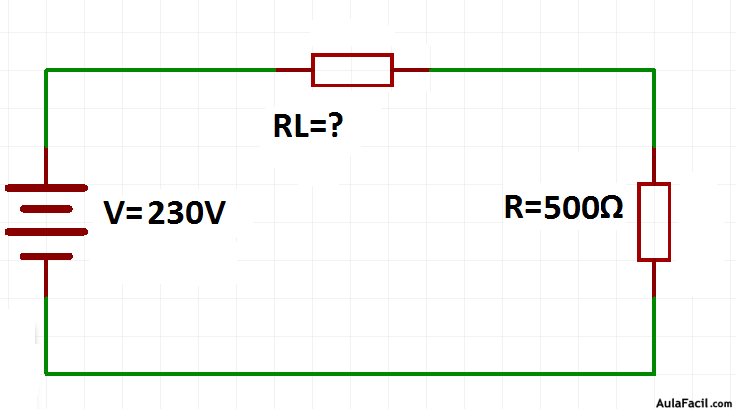
Figura 4
| 1) | RL=Ω | Resistencia del conductor (con solo dos decimales) |
| 2) | I=A | Al valor de la resistencia del cable se le suma el de la resistencia (es un circuito serie que se ve más adelante) |
| 3) | Pperdida=W | Un sólo decimal. Se halla con la fórmula de la potencia (Ver ley de ohm) |
| 4) | PR=W | Un solo decimal |
| 5) | η=% | En porcentaje y un decimal |
Corregir
Ver Solución
Limpiar | ||
- Si se aumenta el voltaje a 1000V en el circuito anterior y se quiere que en la resistencia siga habiendo la misma potencia. Calcular la nueva intensidad que circula por el circuito, la resistencia de carga y la potencia perdida en el cable.
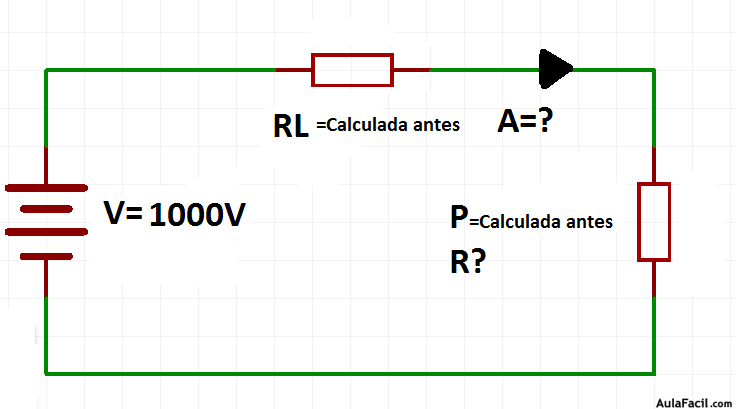
Figura5
| 1) | I=A | Introducir solo un decimal |
| 2) | R=Ω | |
| 3) | Pperdida=W | Introducir cuatro decimales. |
| 4) | η=% | En porcentaje y un decimal |
Corregir
Ver Solución
Limpiar | ||
Como se puede observar, en el segundo caso, al aumentar el voltaje y calcular los ohmios necesarios para obtener la misma potencia en la resistencia de carga que en el caso anterior, conseguimos unas pérdidas menores en el cable. Este es el fundamento de las líneas eléctricas que llevan la misma a casa.
- Se tiene una bombilla alimentada con 230V y de Pmax=100W. A 20ºC su resistencia es de 50.4Ω. Calcular la temperatura a la que brilla la bombilla. Coeficiente de temperatura para el Wolframio:4.1*10-3
Mediante el uso de esta fórmula fácilmente sacamos la temperatura final del filamento de la bombilla:
| 1) | Rn=Ω | Resistencia a la que trabaja la bombilla (Rn=V2/P) |
| 2) | Δt=ºC | Introducir solamente dos decimales |
| 3) | tf=ºC | Introducir solamente dos decimales |
Corregir
Ver Solución
Limpiar | ||