Operación de simetría
Leyes geométricas- matemáticas
Simetría entre los griegos, es la adecuación de las partes del todo, según leyes armónicas. Más actualmente, se concibe la simetría como un procedimiento sistemático de organización basado en leyes especificas, es decir, evidentes.
La simetría se concreta a través de cuatro operaciones:
a) Traslación
La traslación es una sucesión de motivos e intervalos a través de un eje recto, quebrado o curvo. Esa trayectoria tiene su simbolismo por la sucesión en el tiempo a través de ls impulsos vitales de los acontecimientos de lso ciclos cósmicos y de las vivencias del sujeto.
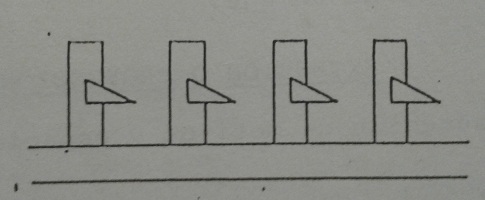
b) Rotación
La simetría por rotación determina un campo espacial y estructural alrededor de un punto, centro o eje de rotación. A la vez esta estructura concéntrica determina tanto el movimiento centrifugo (hacia afuera) como el centrípeto (hacia adentro)
El simbolismo de las estructuras concéntricas o radiales, tiene que ver con la noción del eje del mundo, persistencia del yo intimo, encuadre y protección.
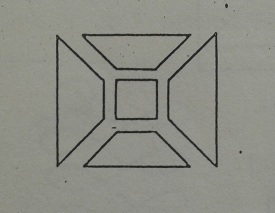

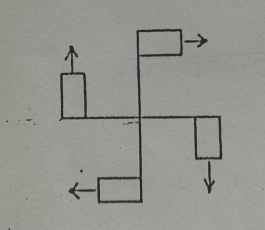
Ejes de rotación
c) Reflexión especular
Tiene que ver con todas las cuestiones de la estabilidad y del equilibrio axial. También se la define como un retrato bilateral y la compensación de estructuras a través de un eje.
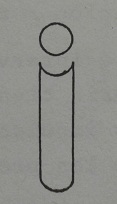
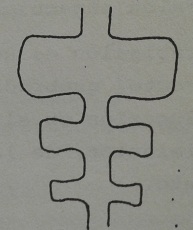
d) Extensión o proyección
Implica una sucesión de motivos y espacios en un orden, sea creciente o decreciente.

e) Combinaciones de leyes geométricas nombradas
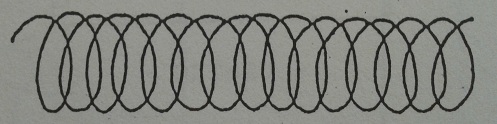
1. Traslación rotativa (movimiento helicoidal)
2. Traslación refleja
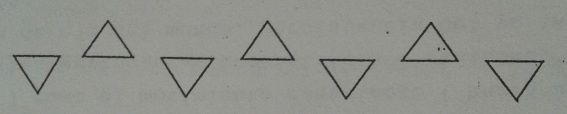
3. Extensión traslatoria




