Tipos de Rectas: Paralelas y Perpendiculares

Dos rectas en el espacio tienen unas posiciones relativas, es decir, pueden cruzarse, cortarse o ser paralelas.

Si dos rectas se cruzan no llegan nunca a cortarse, no tienen punto en común.

Por ejemplo, pintamos una recta en el río y otra en el puente. Si las miramos desde arriba se cruzan pero nunca llegan a cortarse.

Cuando dos rectas se cortan tienen un mismo punto en común.

Dependiendo de cómo se corten dos rectas pueden ser perpendiculares o secantes:

Dos rectas son secantes cuando se cortan y entre las dos rectas forman un ángulo cualquiera.

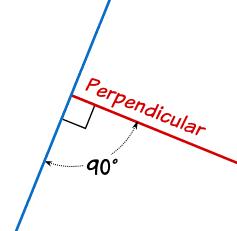
Dos rectas son perpendiculares cuando se cortan ortogonalmente en un punto, es decir, cuando las dos rectas forman 90 grados.

Dos rectas son paralelas cuando se cortan en el infinito. La distancias entre sus puntos son las mismas.

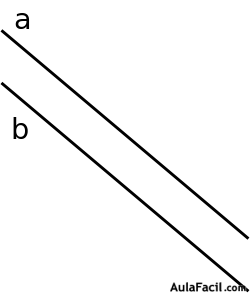
Para explicar esto os pongo el ejemplo de las vías del tren, están formadas por los raíles, que no se cortan, pero que cuando los miramos con perspectiva vemos que se unen y se cortan en el infinito.

Ahora bien, en el formato papel se pueden representar estas rectas y sus posiciones relativas mediante la escuadra y el cartabón:

Para trazar una recta paralela (B) a otra dada (A) se pone un cateto de la escuadra sobre la recta y la hipotenusa sobre la hipotenusa del cartabón (la hipotenusa es el lado más largo de un triángulo rectángulo).

Trazamos una recta (A) por uno de los catetos y deslizamos la regla hasta la posición deseada, y volvemos a trazar una recta (B) que en este caso será paralela a la anterior.

Para trazar una recta (D) perpendicular a otra dada (C) la teoría es la misma, se dibuja una recta cualquiera por un cateto y se desliza hasta la altura deseada, pero la nueva recta se traza por el otro cateto de la recta.

Por pasos:

• Paso 1:

• Paso 2: