Finales con muchos peones II

Finales de Alfiles
Finales con muchos peones

(Guillermo Gutiérrez)

Para resolver posiciones bloqueadas complicadas se puede aplicar con éxito el método de las "casillas conjugadas". Analicemos el siguiente ejemplo.

En la posición, las blancas tienen que transmitir el turno de jugar a su adversario, ya que ante 1...Ad6 ó 1...Af8 decide 2.Ac1, Ae7; 3. Ae3, capturando un peón. ¿Qué casilla es la que está conjugada con la de b2? Evidentemente la f6. Si el alfil se hallase en d6, las blancas ganaban inmediatamente moviendo 1.Ac1, Ae7; 2.Ae3, etc. Al escaque c1 corresponde únicamente el d8. Al d2, el f6. ¿Qué casilla está conjugada con la e8? No es la h8, ya que después de la jugada 1.Af2, Ae7; 2.Ae3, las blancas ceden inmediatamente el turno de jugar; tampoco la e2, ya que a continuación de 1.Ac3, Af6; 2.Ab2, Ae7; 3.Aa3!, Af8; 4.Ac1!, Ae7; 5.Ae3, la transmisión del turno de jugar tiene también lugar. Por consiguiente, el escaque e1 se encuentra conjugado únicamente con el g7. Entonces es evidente que con la casilla c3 está conjugada h8; con la f2 la f8, y con la a1 la g7. Intentemos ahora encontrar el escaque conjugado con la casilla g3. Debe ser la casilla g7. Pero con ésta última se halla conjugada también la e1. Veamos, pues, que las blancas tienen dos escaques iguales, con la particularidad que se puede pasar de uno a otro con un solo movimiento. Luego, las negras no pueden mantener la conjugación. Establezcamos el cuadro de las casillas conjugadas:

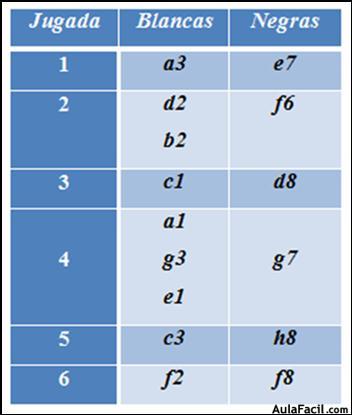
Mirando la tabla se pude formular directamente la resolución: 1.Ab2 (1.Ac1 Ad8! 2.Ad2 Af6! 3.Ae1! Ag7! 4.Ag3!! Af6 5.Af2 Ae7 6.Ae3 y un peón será eliminado del tablero; a simples tablas conduce 1.b4?? cxb4 2.Axb4 Axb4 3.Rxb4 y el rey blanco no puede pasar) 1...Af6! 2.Ac3 Ah8! 3.Ae1! Ag7! 4.Ag3!! Af6 5.Af2 Ae7 6.Ae3 (1–0) y ahora las negras pierden uno de los dos peones.