Como estamos viendo, dos ejes cartesianos son dos rectas perpendiculares que dividen a un plano en cuatro partes, cuatro zonas, cuatro cuadrantes. El punto donde se cortan estos dos ejes llamamos origen de coordenadas.
En estos cuadrantes representamos los puntos y el origen de coordenadas se encuentra en el punto cero (el punto donde se cortan los dos ejes).
Los puntos se refieren primero, al valor de la abscisa o eje x se le agrega una coma y a continuación se escribe el valor de la ordenada o eje y.
Los cuadrantes se numeran en el sentido contrario a la marcha de las agujas de un reloj.
En el PRIMER CUADRANTE la abscisa es positiva y la ordenada también.
En el SEGUNDO CUADRANTE la abscisa es negativa y la ordenada positiva.
En el TERCER CUADRANTE la abscisa es negativa y la ordenada también.
En el CUARTO CUADRANTE la abscisa es negativa y la ordenada positiva.
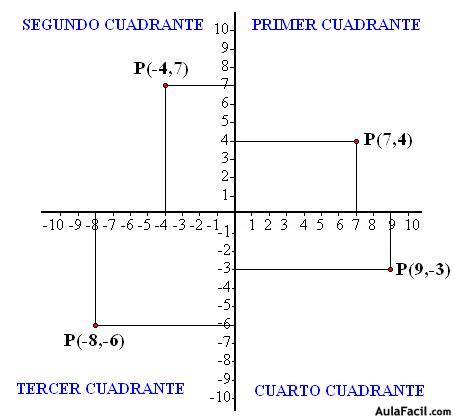
A continuación tienes la numeración de los cuadrantes y cuatro puntos representados, uno en cada cuadrante:
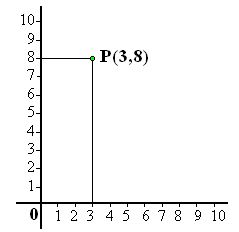
8.1 Dibuja el primer cuadrante y coloca el punto (3,8)
Respuesta:
Como comprobarás hemos hecho uso solamente del primer cuadrante. No hace falta más para representar del punto solicitado.
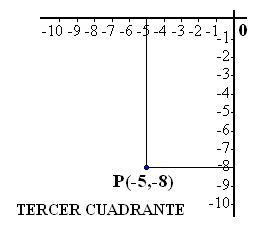
8.2 Dibuja el tercer cuadrante y coloca el punto (-5,-8)
Respuesta:
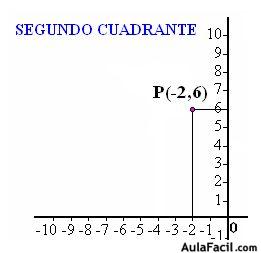
8.3 Dibuja el segundo cuadrante y coloca el punto (-2,6)
Respuesta:
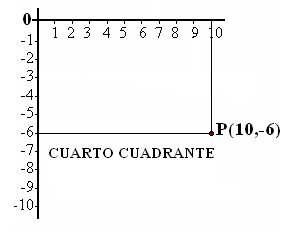
8.4 Dibuja el cuarto cuadrante y coloca el punto (10,-6)
Respuesta:
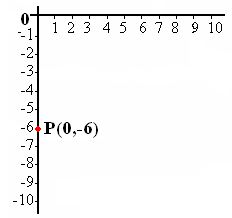
8.5 Sitúa el punto (0,-6)
Respuesta: Como el cero, tanto para la abscisa como para la ordenada se encuentra en el punto donde se cortan los dos ejes tendremos que el valor de x es cero y el valor de y -6:
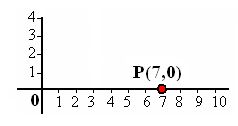
8.6 Sitúa el punto (7,0)
Respuesta: En este caso vemos que el valor de abscisa o x es 7 y el de ordenada o y es cero cuyo valor se encuentra en el punto donde se cortan las rectas de abscisas y ordenadas:
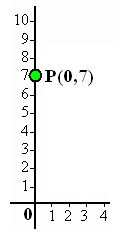
8.7 Coloca el punto (0,7)
Respuesta:
En éste caso el valor de abscisa es cero.
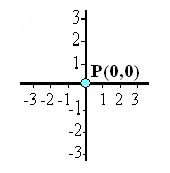
8.8 ¿Dónde colocas el punto P(0,0)?
Respuesta: Como los dos valores son iguales a cero, se encontrará exactamente en el punto de corte de ambas perpendiculares: