Clasificación de los Triángulos según sus ángulos - Relación entre los ángulos y los lados de los triángulos
Se dividen en:
1) Triángulos rectángulos si tienen UN ángulo recto.
Tienes a continuación tres ejemplos de triángulos rectángulos
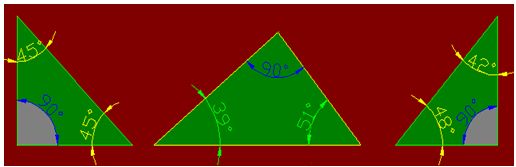
En un triángulo rectángulo, el lado opuesto al ángulo recto se llama hipotenusa y los lados perpendiculares que forman el ángulo recto se llaman catetos.
Teorema de Pitágoras: Al estudiar el triángulo rectángulo hemos de conocer perfectamente este teorema que nos dice:
En todo triángulo rectángulo, la suma de los cuadrado de los catetos es igual al cuadrado de la hipotenusa
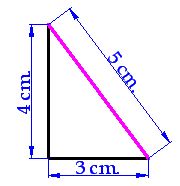
Tomemos como ejemplo el de la figura en el que los catetos miden 3 y 4 cm., respectivamente y 5 cm., la hipotenusa.
Con las medidas de los catetos formamos cuadrados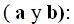 
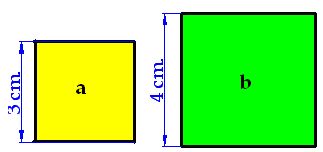
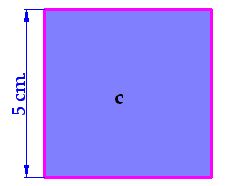
Con la longitud de la hipotenusa formamos otro cuadrado (c):
Si calculas el área del cuadrado formado por el cateto (a): lado al cuadrado obtienes como valor del área: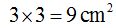 
Si a continuación calculas el cuadrado formado por el cateto (b), el valor de su área vale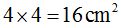 
El cuadrado formado por la longitud de la hipotenusa tiene un área de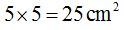 
Si sumas las áreas de los cuadrados de los catetos, es decir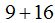 
obtienes el área formada por el cuadrado de la hipotenusa,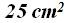 
Fíjate en la figura siguiente:
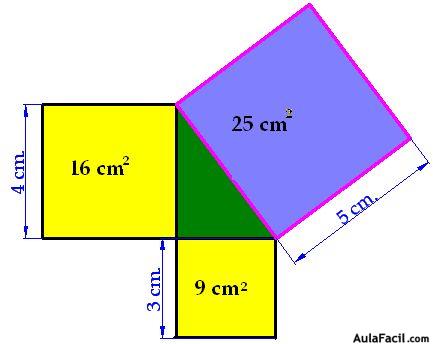
La suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa.Siendo a y b las longitudes de los catetos los catetos, y c la longitud de la hipotenusa podemos escribir:
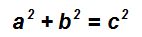
Resuelve:
(a) Calcula la longitud de la hipotenusa de un triángulo rectángulo sabiendo que los catetos miden 5 y 6 cm., respectivamente.
El resultado es de 7,81 cm. porque la suma de los cuadrados de los catetos es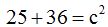 
de donde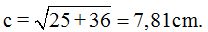 
(b) Sabiendo que la hipotenusa de un triángulo rectángulo vale 10 cm., y uno de los catetos 8 cm.
¿Cuál es el valor del otro cateto?
El resultado es de 6 cm. Porque
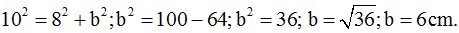
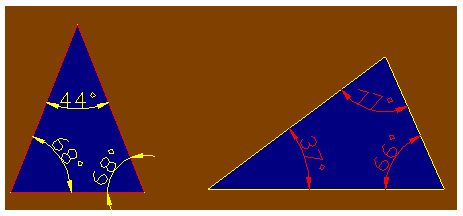
2) Triángulos acutángulos, si tienen TRES ángulos agudos(menores de 90º).
En el dibujo siguiente tienes dos triángulos acutángulos.
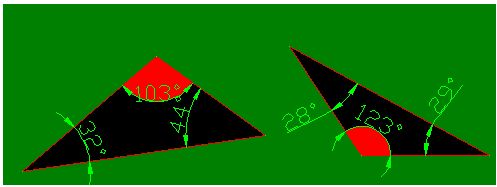
3) Triángulos obtusángulos, si tienen UN ángulo obtuso (más de 90º).
En la siguiente figura tienes dos triángulos obtusángulos
15.76 ¿Puede un triángulo rectángulo tener, además de su ángulo recto, dos ángulos de 56º y 45º? ¿Por qué?
Respuesta: No, porque la suma de los tres ángulos debe valer 180º y en este caso, supera ese número.
15.77 Dos triángulos isósceles tienen iguales dos lados y el ángulo comprendido entre ellos. ¿Son necesariamente iguales?
Respuesta: Sí.
15.78 ¿La suma de los ángulos no rectos de los triángulos rectángulos han de sumar un ángulo recto? ¿Por qué?
Respuesta: Sí, porque si el ángulo recto vale 90º los otros dos 2 ángulos no rectos tendrán que sumar 90º, de este modo, la suma de los ángulos del triángulo suman 180º
RELACIÓN ENTRE LOS ÁNGULOS Y LOS LADOS DE LOS TRIÁNGULOS
En los triángulos los ángulos dependen de los lados en cuanto a sus medidas, de ahí que podemos decir:
A) A mayor lado se opone mayor ángulo
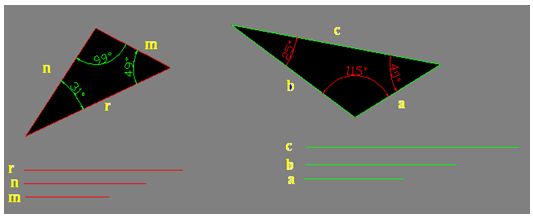
Comprueba en la figura siguiente que a mayor lado, se oponemayor ángulo.
Lo mismo puede decirse a la inversa, a menor ángulo, se opone menor longitud de lado
B) En un triángulo, la longitud de un lado cualquiera es menor que la suma de las longitudes de los otros dos lados.
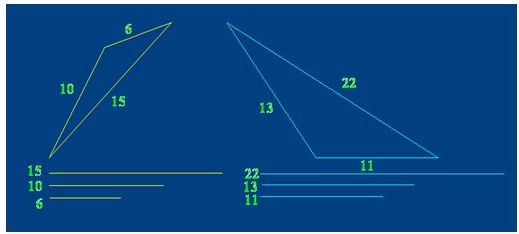
La suma de los dos lados menores será siempre mayor que el lado más grande.
En el primer triángulo la suma de los lados de menor longitud es mayor que la del lado de mayor longitud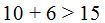 
Lo mismo sucede en el segundo triángulo de la figura: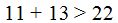 
C) Si un triángulo tiene sus lados iguales también serán sus ángulos opuestos.
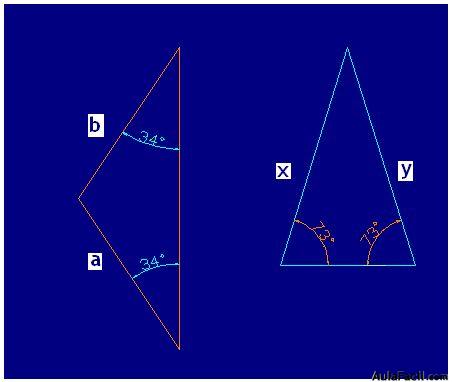
En la figura siguiente verás en el primer triángulo que los lados a y b al tener iguales longitudes, sus ángulos opuestos miden lo mismo.
Igualmente, en el segundo triángulo los lados x e y al tener la misma longitud, sus ángulos opuestos son iguales.
