Ángulos de lados Paralelos - Ángulo de lados Perpendiculares- Bisectriz de un ángulo
ÁNGULOS DE LADOS PARALELOS
A) Dos ángulos de lados paralelos, los dos agudos o los dos obtusos, son iguales.
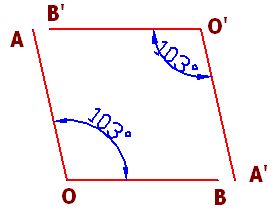
Los ángulos 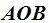 y A’O’B’ tienen sus lados paralelos (los lados OA y O’A’ son paralelos entre sí, como también lo son OB y O’B’).Los dos ángulos son obtusos y vemos que son iguales.
y A’O’B’ tienen sus lados paralelos (los lados OA y O’A’ son paralelos entre sí, como también lo son OB y O’B’).Los dos ángulos son obtusos y vemos que son iguales.
B) Si los lados de ambos ángulos, uno obtuso y otro agudo tiene sus lados paralelos (OA paralelo con O’A’, OB paralelo con O’B’) son suplementarios.
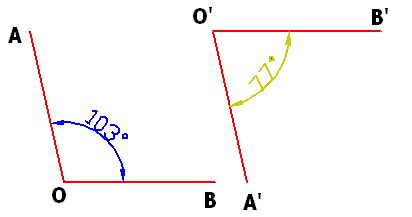
Si sumas ambos ángulos comprobarás que el resultado es de 180º, es decir, son suplementarios.
ÁNGULOS DE LADOS PERPENDICULARES
Igual que en el caso anterior, podemos considerar que los ángulos sean los dos obtusos o los dos agudos y que uno sea obtuso y el otro agudo o viceversa.
A) En el caso de que ambos ángulos sean agudos o ambos obtusos y sus lados perpendiculares tienen el mismo valor.
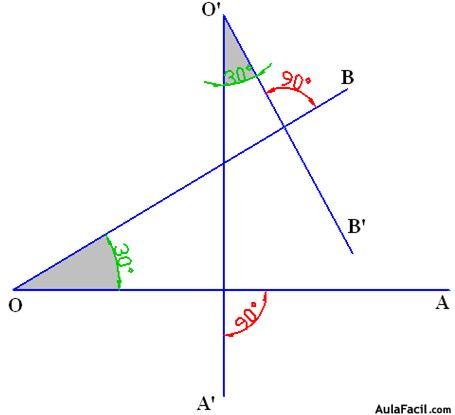
Observa que los lados de ambos ángulos son perpendiculares entre sí; el lado OA es perpendicular al lado O’A’ y el OB es perpendicular al lado O’B’. Vemos que cuando se dan las condiciones anteriores, los ángulos son IGUALES (en el ejemplo, 30º).
B) Si los lados de ambos ángulos, uno agudo y el otro obtuso son perpendiculares, los ángulos son suplementarios:
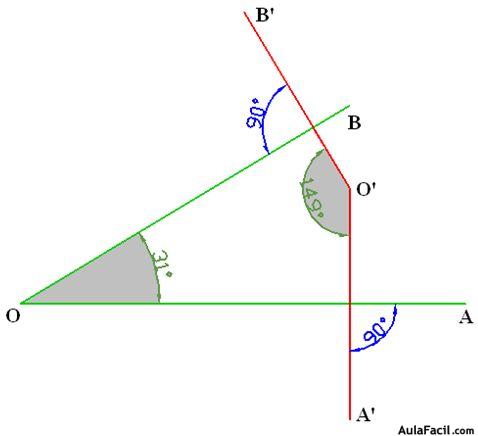
Los lados OA y O’A’ son perpendiculares lo mismo que OB con relación a O’B’ y los ángulos que forman los lados a los que acabamos de hacer referencia, son suplementarios: 31º + 149º = 180º
BISECTRIZ DE UN ÁNGULO
La palabra bisectriz procede del latín bis que significa dos veces y secare que significa cortar.
Se llama bisectriz de un ángulo a la recta que partiendo del vértice divide al ángulo en dos partes iguales:
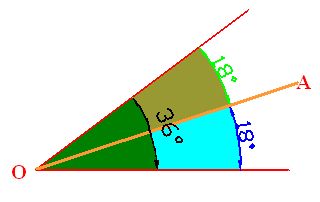
La recta OA es la bisectriz porque al ángulo de 36º lo divide en dos partes iguales de 18º cada una.
15.56 Uno de los ángulos adyacentes mide 100º50’50’’ ¿Cuánto mide el otro?
Respuesta: 79º09’10’’
15.57 ¿Cuánto vale el ángulo que forman las bisectrices de dos ángulos adyacentes?
Respuesta: 90º
Solución:
En la figura tenemos dos ángulos adyacentes uno 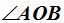 de 135º (en color rojo) y el otro
de 135º (en color rojo) y el otro 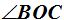 (en color azul claro) de 45º.
(en color azul claro) de 45º.
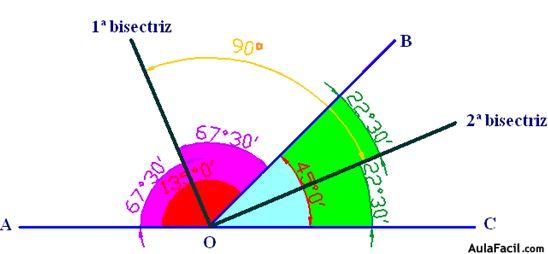
Trazamos las bisectrices de cada uno de los ángulos y el ángulo obtuso de 135º se ha dividido en dos ángulos que miden 67º30’ cada uno y el ángulo agudo de 45º ha quedado dividido por su bisectriz en dos ángulos de 22º30’ cada uno.
Midiendo el ángulo que forman las dos bisectrices comprobamos que su medida angular equivale a 90º.
No importa la medida de los ángulos adyacentes, la medida angular de sus bisectrices será de 90º
15.58 ¿Cuánto valen cada uno de los ángulos que forman dos rectas perpendiculares?
Respuesta: 90º
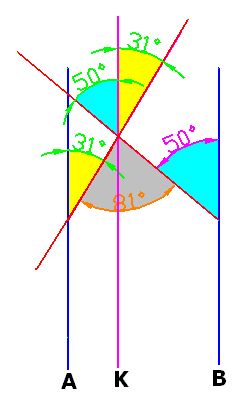
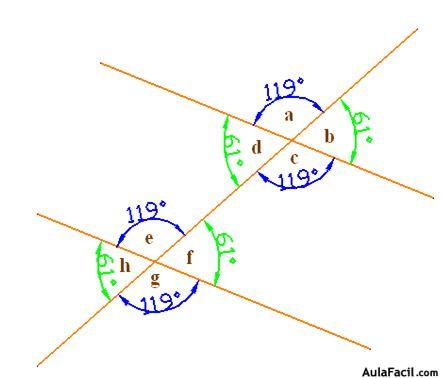
15.59 Tenemos dos rectas paralelas cortadas por una recta secante. Uno de los ángulos vale 119º. ¿Cuánto valen los otros siete?
Respuesta: a) 119º; b) 61º; c) 119º; d) 61º; e) 119º; f) 61º; g) 119º; h) 61º
Solución:
Gráficamente tenemos:
15.60 En la figura:
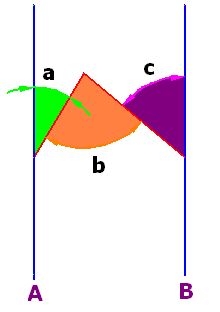
Demuestra que la suma de los ángulos a y c son iguales al ángulo 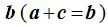
Solución:
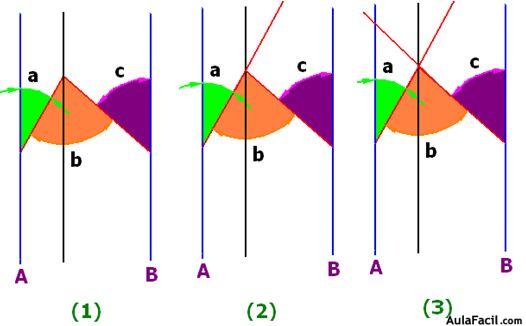
En (1) trazo una paralela a la recta A
En (2) prolongo uno de los lados del ángulo a
En (3) prolongo uno de los lados del ángulo c
Los nuevos ángulos que se han formado con las prolongaciones de los lados corresponden a a’ y c’ que son iguales a los ángulos
a y c por correspondientes (al mismo lado de la secante y ambos internos).
En este caso, las paralelas las forman las rectas A y K.
Lo dicho anteriormente puedes comprobarlo en la figura siguiente:
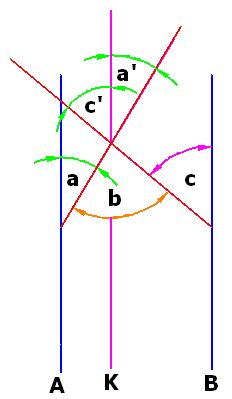
Verás que la suma de los ángulos a’ y c’ son iguales al ángulo b por opuestos por el vértice.
Haciendo las mediciones de los ángulos en la última figura obtenemos: