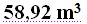Octaedro, Volúmen del Octaedro
Si en cada vértice de un poliedro concurren 4 triángulos equiláteros entonces obtenemos un OCTAEDRO (octa = 8, edros = caras):
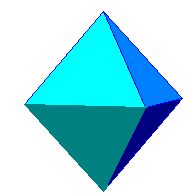
Cada vértice poliédrico vale 60º x 4 = 240º , es decir, menos de 360º.
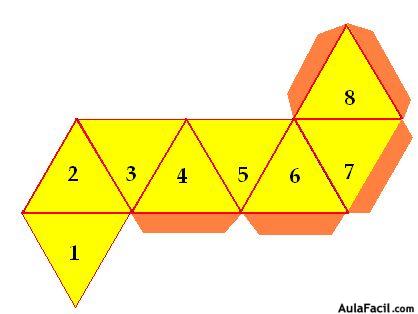
Construye un octaedro:
Sirviéndote de una cartulina, tijeras, reglas y pegamento dibuja 8 triángulos equiláteros con sus correspondientes solapas.
Corta la cartulina por el contorno del dibujo.
Dobla la cartulina por las líneas del contorno de los triángulos y solapas.
Extiende el pegamento por encima de las solapas y después las pegas.
15(3).12 ¿Cuántos vértices tiene un octaedro?
Respuesta: 6 vértices
15(3).13 ¿Cuántas aristas tiene un octaedro?
Respuesta: 12 aristas
15(3).14 ¿Cuántas caras concurren en un vértice del octaedro?
Respuesta: 4 caras
VOLUMEN DEL OCTAEDRO.
Vamos a deducir la fórmula y para ello nos servimos de lo estudiado en el cálculo del volumen del tetraedro.
En la siguiente figura hemos dibujado un octaedro:
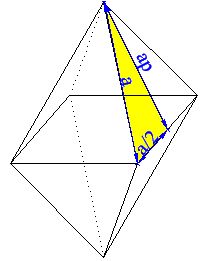
En primer lugar calculamos el valor de la apotema. El triángulo rectángulo en color amarillo nos muestra un cateto que es la apotema (ap), la arista (a) que es la hipotenusa y el segundo cateto (a/2). Aplicando el teorema de Pitágoras:
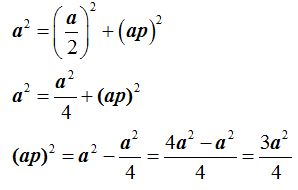
Extraemos la raíz cuadrada en ambos términos de la igualdad:
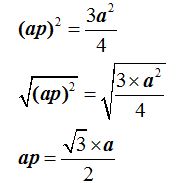
Ahora vamos a calcular el área de una cara:
Conocemos la base del triángulo equilátero que es una de sus 8 caras (a) y conocemos la altura del triángulo (ap):
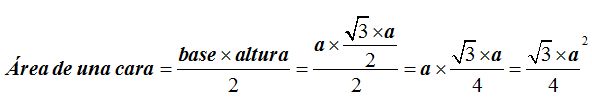
Para calcular el volumen vas a fijarte en la figura que tienes a continuación:
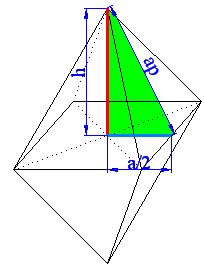
El triángulo rectángulo de color verde tiene como hipotenusa el valor de la ap (apotema) , uno de los catetos es la altura de la mitad del octaedro que lo hemos representado por (h).
El otro cateto vale la mitad de la arista, es decir 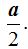
En la siguiente figura puedes ver una aclaración:
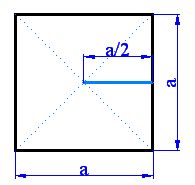
En esta última figura ves que uno de los catetos vale 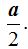
La altura h de la mitad del octaedro vale teniendo en cuenta el teorema de Pitágoras:
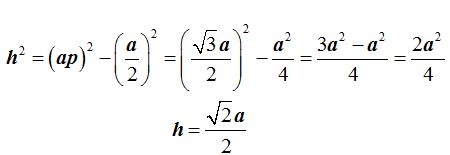
La mitad del octaedro sería incluyendo los datos que nos interesan:
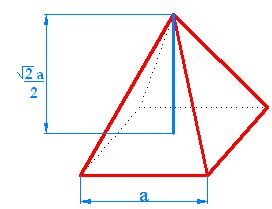
Fíjate qirue la base de esta mitad del octaedro es un cuadrado que tiene un lado cuyo valor es el de la arista (a).
El volumen de este semioctaedro será, teniendo en cuenta que se trata de un poliedro y no un prisma (tenemos que dividir por 3):
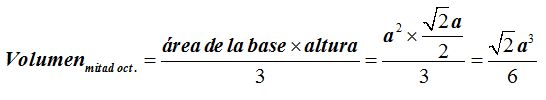
El volumen del octaedro será el doble, es decir:
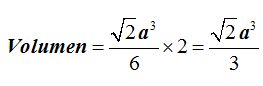
15(3).15 Halla el volumen de un octaedro de 5 m. de arista.
Respuesta: