Proporcionalidad Inversa o Regla de Tres Inversa
El inverso de un número se representa por la unidad dividida por dicho número:
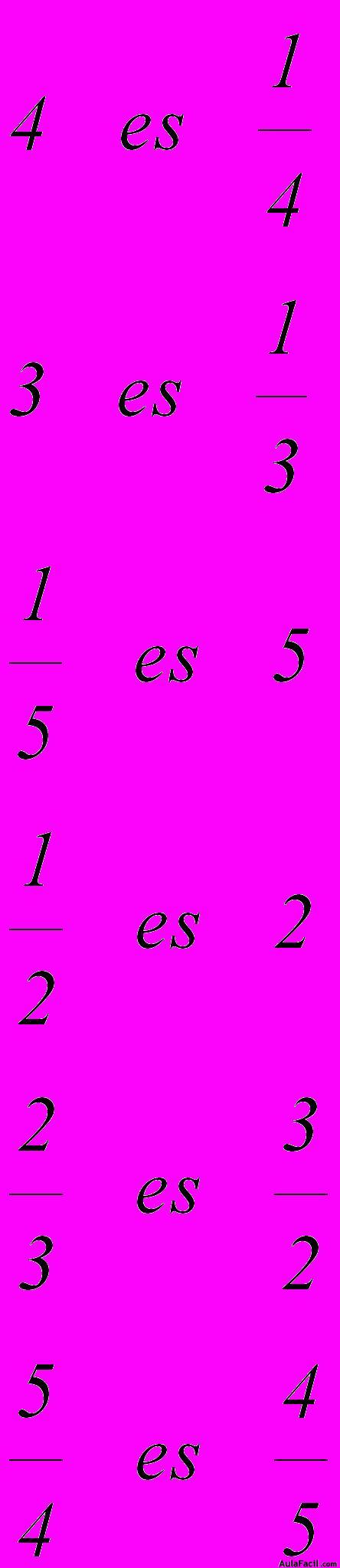
Siempre dividimos la unidad por el número. Para calcular el inverso de 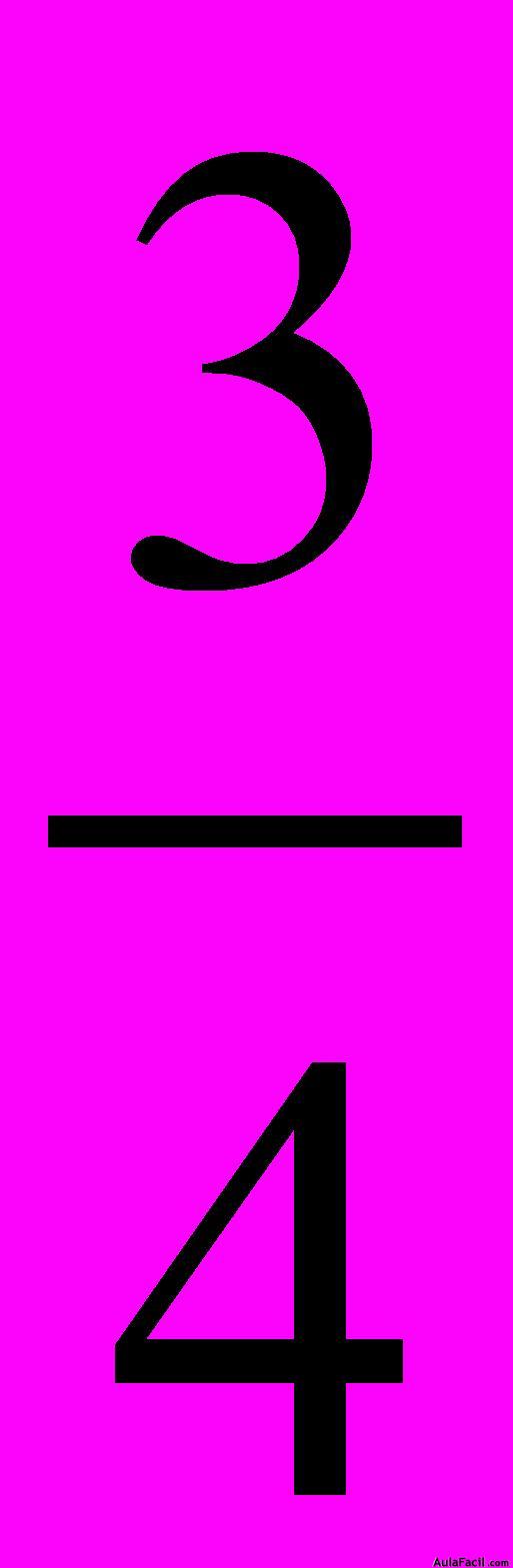 dividimos 1 entre
dividimos 1 entre 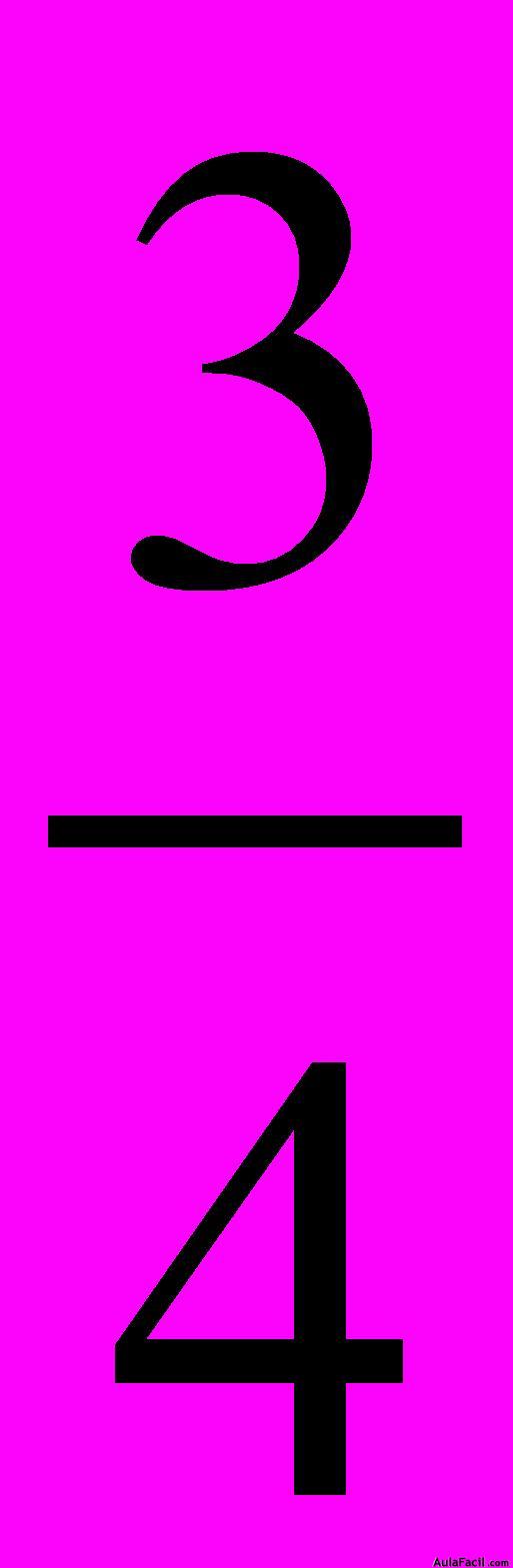 y escribimos:
y escribimos: .
.
Al 1 del numerador lo podemos dividir por 1 sin que haya variado ningún valor y escribiremos:

Es importante que lo que acabamos de decir lo tengas muy en cuenta. Veamos como resolvemos un problema de proporcionalidad inversa o regla de tres inversa.
6.42 Un carpintero construye 9 mesas en 3 días trabajando 6 horas al día. ¿Cuántos días necesitará para hacer el mismo número de mesas si trabaja 9 horas al día?
Respuesta: 2 días
Solución:
Lo resolvemos primero por regla de tres:

(a más horas de trabajo al día necesitará menos días inversa)
inversa)
Resolvemos con proporciones:
Con los datos que tenemos establecemos las dos razones o cocientes:  por lo que se refiere a los días y
por lo que se refiere a los días y  por lo que se refiere a las horas de trabajo por día. Pero como se trata de una proporcionalidad inversa invertimos los datos de una razón;
por lo que se refiere a las horas de trabajo por día. Pero como se trata de una proporcionalidad inversa invertimos los datos de una razón;
hallamos el inverso de que es
que es 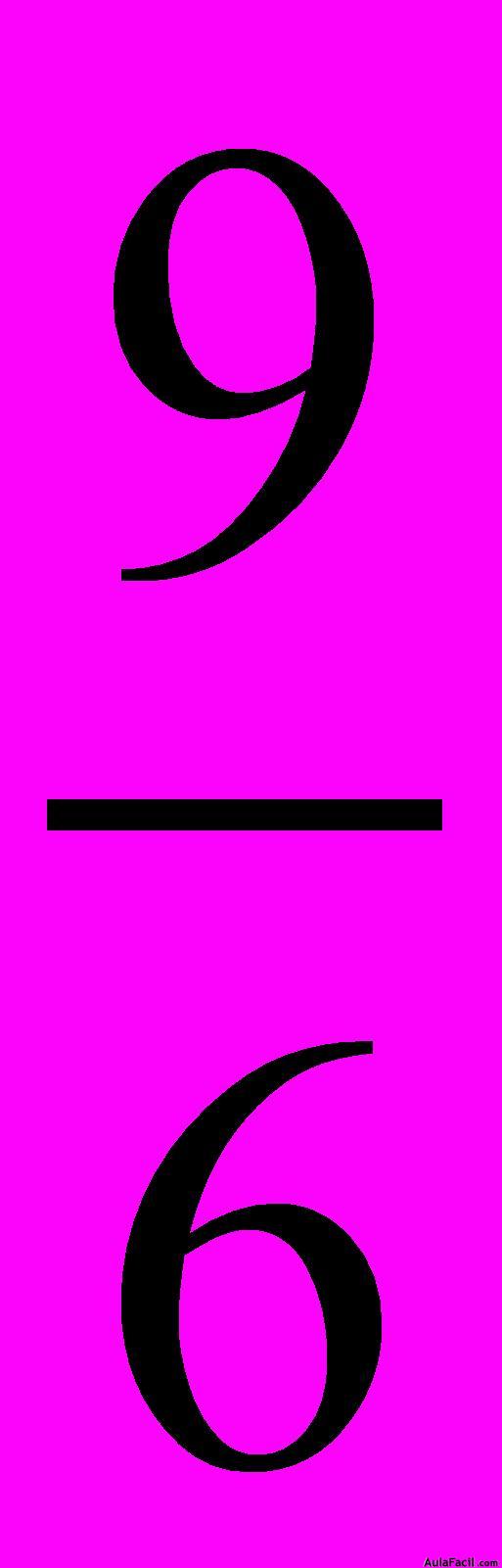 .
.
La proporción correcta para la resolución de este problema es: 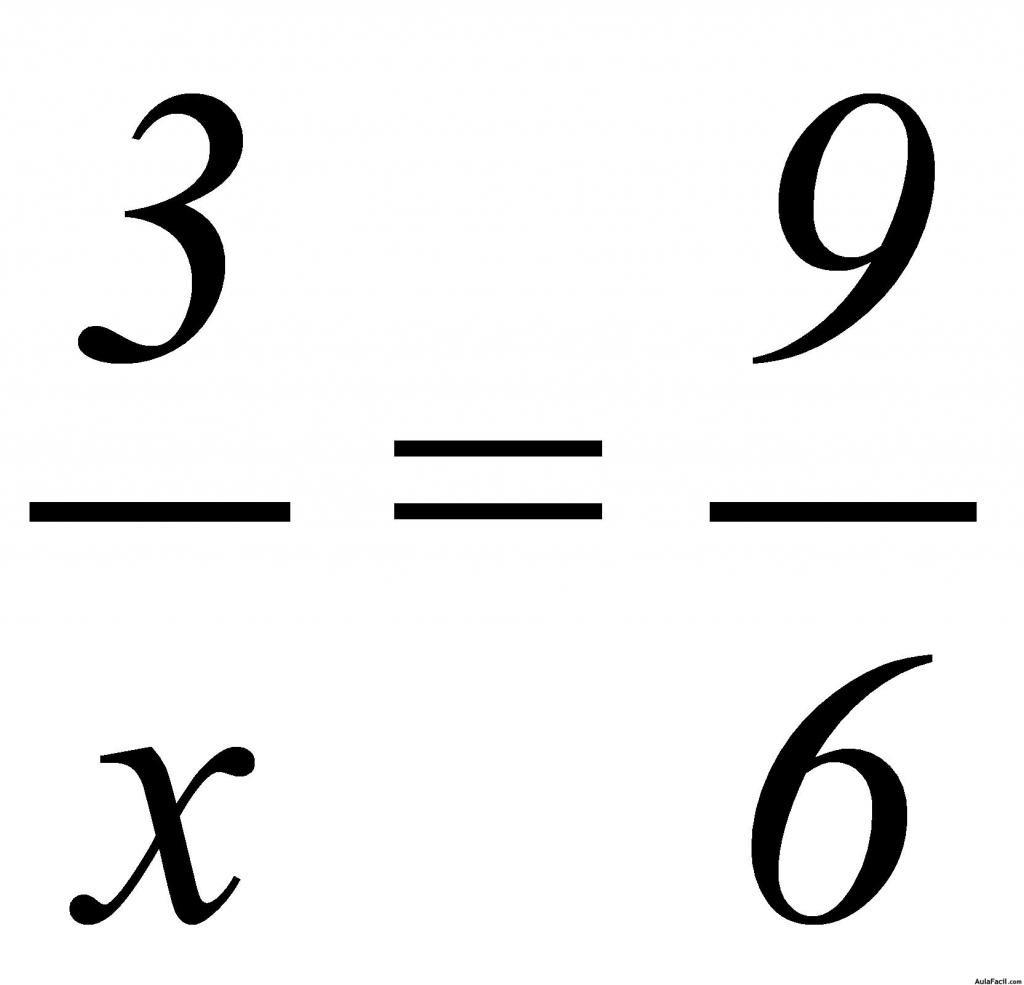
Producto de extremos igual al producto de medios: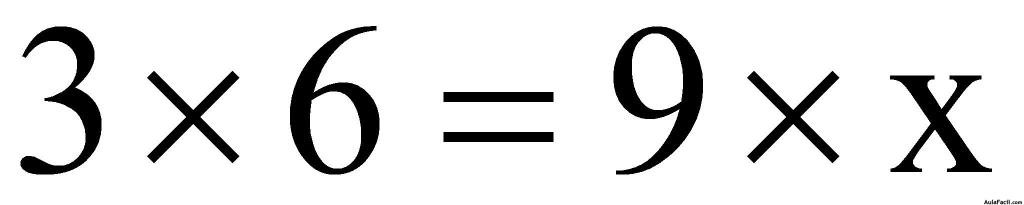
de donde
6.43 Un coche recorre hace un recorrido en 3 horas marchando a una velocidad de 100 Km/h. ¿Cuántas horas tardaría si va a una velocidad de 150 Km/h.?
Respuesta: 2 horas
Solución:
Calculamos por medio de una proporción:
Las razones son: 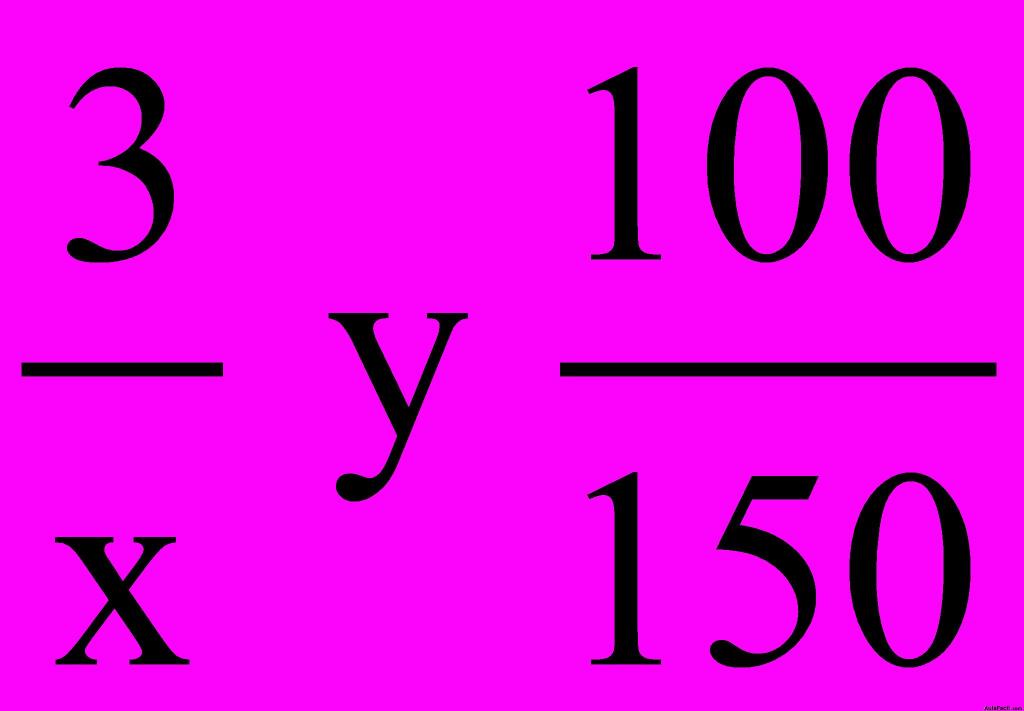 pero como sabemos que a más velocidad tardará menos tiempo, hallamos el inverso de la segunda razón y así tenemos:
pero como sabemos que a más velocidad tardará menos tiempo, hallamos el inverso de la segunda razón y así tenemos: 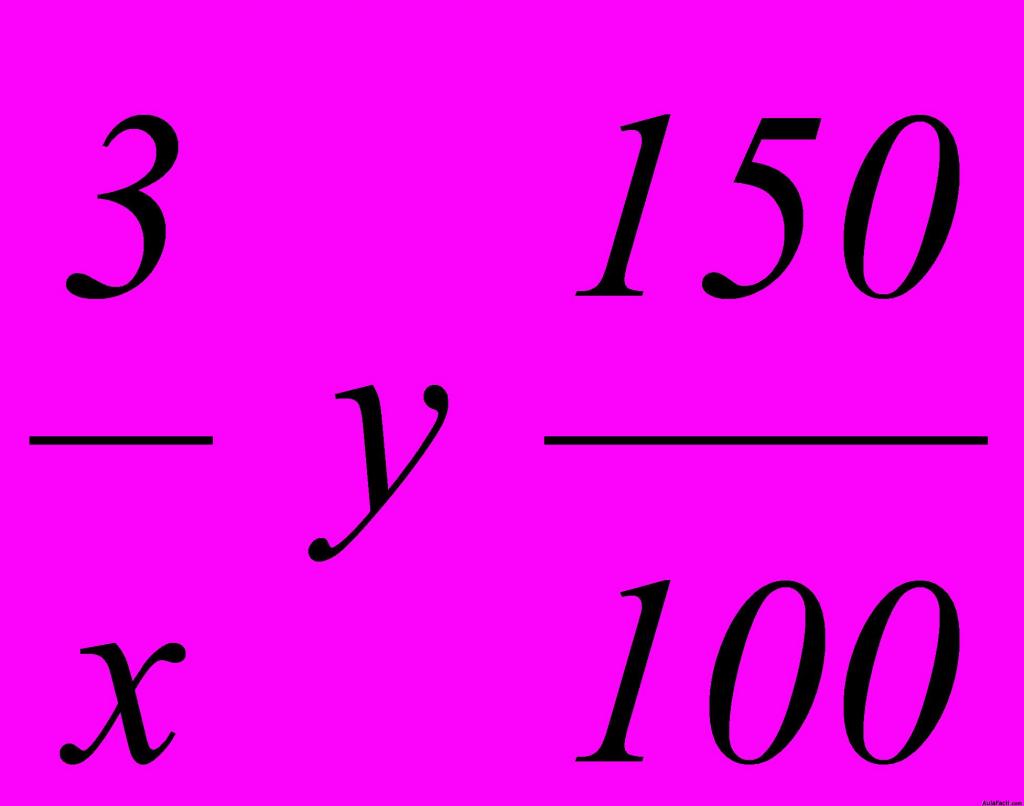 . Establecemos la proporción y la resolvemos:
. Establecemos la proporción y la resolvemos: 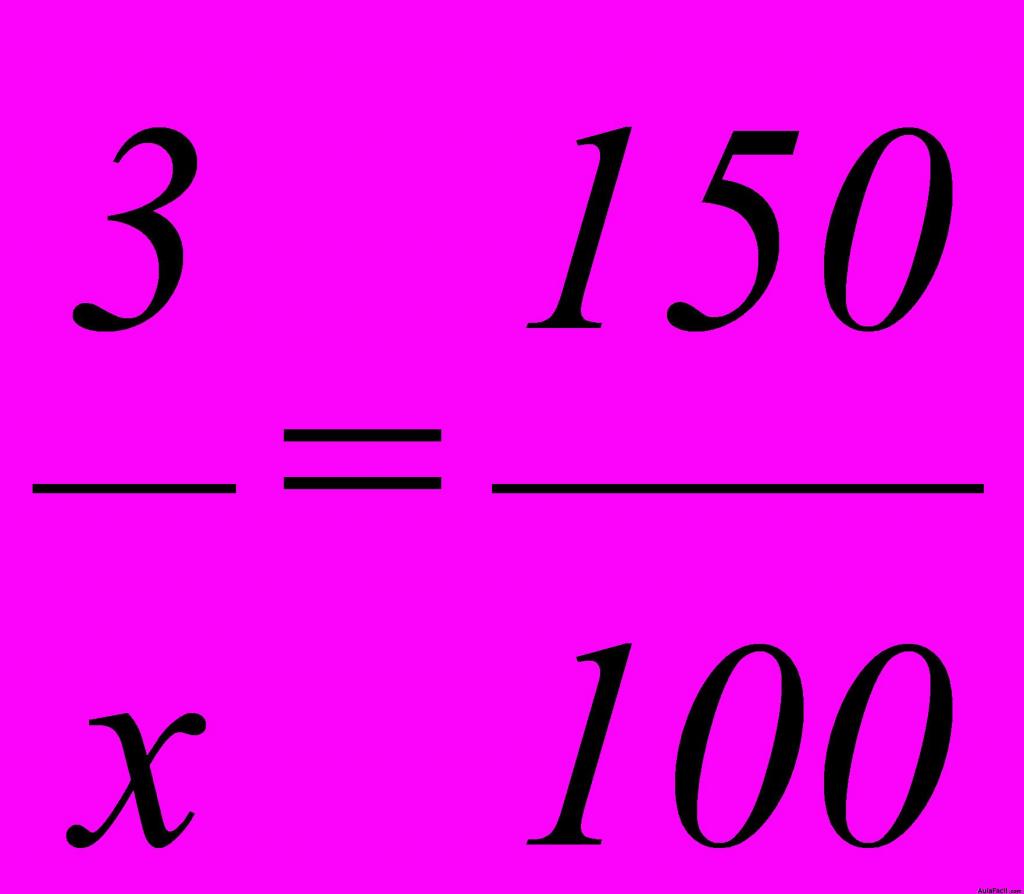 ,
, 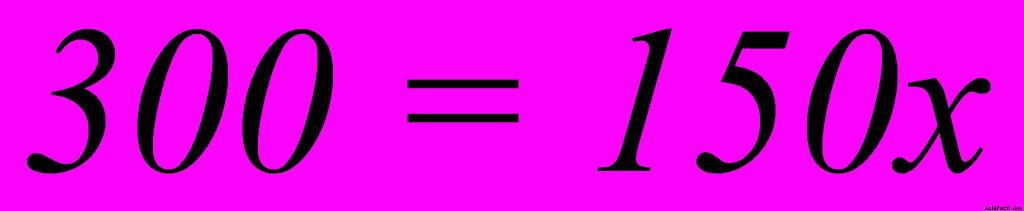 de donde
de donde
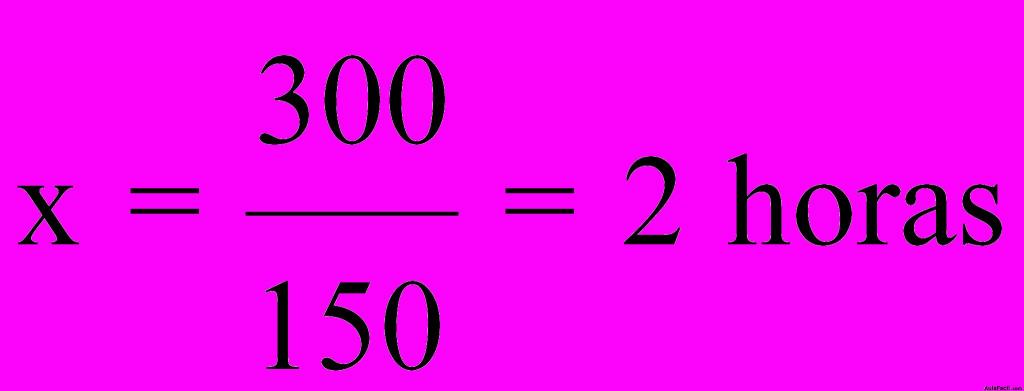
6.44 Calcula el número de días que hubieran necesitado 20 obreros para hacer un trabajo que otro grupo de 30 necesitó 10 días.
Respuesta: 15 días

