Teorema de Pitágoras
Ahora bien, para empezar a estudiar las Funciones Trigonométricas, es necesario dominar lo que en Matemáticas se conoce como el Teorema de Pitágoras, para ello, nos familiarizaremos con algunos de sus términos descritos a continuación:
“En un Triángulo Rectángulo el Cuadrado de la Hipotenusa es igual a la suma de los Cuadrados de sus Catetos”.
Simbólicamente se describe así:
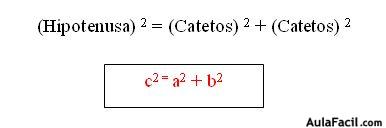
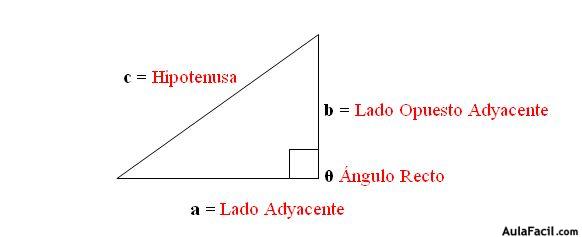
Los lados Adyacentes en un Triángulo Rectángulo se denominan Catetos, y el Lado Opuesto al Ángulo recto se llama Hipotenusa.
El Teorema de Pitágoras en sí, lo utilizamos para encontrar variables desconocidas, y éstas pueden ser los Lados Adyacentes o bien, la Hipotenusa.
Empecemos a trabajar con un ejemplo sencillo:
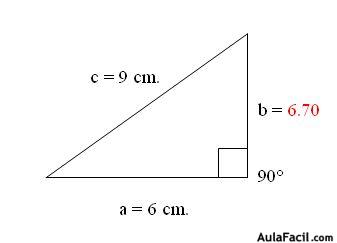
1. Se tienen los lados de un Triángulo Rectángulo a = 6 cm. y b = 6.7 cm, lado c = 9 cm.
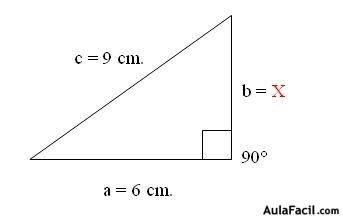
Cómo nos damos cuenta, tenemos una incógnita que debemos encontrar el valor, ésta será nuestra variable X. Aplicando el Teorema de Pitágoras, procedemos a utilizar la Fórmula:
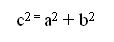
1. Empezamos por sustituir las cantidades numéricas en las variables correspondientes
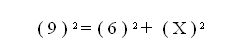
2. Realizamos las operaciones:
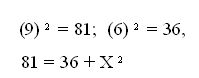
3. Procedemos a despejar la Ecuación, a modo de dejar sola la variable que queremos encontrar:
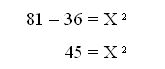
4. Para dejar la Variable sola, pasamos el exponente al otro lado, convirtiéndolo en Radical.
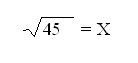
Obtenemos Raíz Cuadrada de 45 dándonos como respuesta 6.70 = X = b
Definición Obtenida de “Aritmética, Teoría Práctica”, Autor Aurelio Baldor, Edición 1978.

