Fracciones

La fracción se utiliza para representar las partes que se toman de un objeto que ha sido dividido en partes iguales.
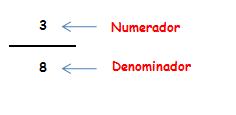
Por ejemplo, dividimos una pizza en 8 partes iguales y cogemos tres. Esto se representa por la siguiente fracción:

Los términos de la fracción se denominan: numerador y denominador.
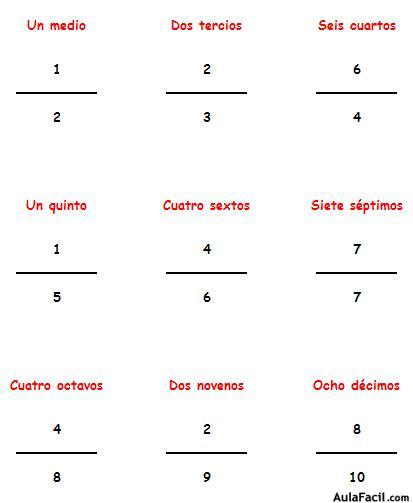
¿Cómo se leen las fracciones? Se leen en función de cuál es su denominador:
1 / 2: un medio
1 / 3: un tercio
1 / 4: un cuarto
1 / 5: un quinto
1 / 6: un sexto
1 / 7: un séptimo
1 / 8: un octavo
1 / 9: un noveno
1 / 10: un décimo
1 / 11: un onceavo
1 / 12: un doceavo
1 / 13: un treceavo
Veamos algunos ejemplos:
¿A cuantas unidades equivale una fracción? Para calcularlo se divide el numerador entre el denominador:
Por ejemplo:
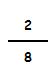
Para ver a cuantas unidades equivale esta fracción dividimos: 2 : 8 = 0,25
Equivale a 0,25 unidades
Si una fracción tiene igual numerador y denominador representa la unidad.
Por ejemplo, divido una tarta en 4 partes y me tomo las cuatro partes:
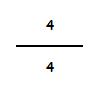
Quiere decir que me he tomado la totalidad de la tarta (4 / 4), lo que equivale a la unidad (a la tarta). Si dividimos 4 : 4 = 1

1.- Fracciones equivalentes
Dos fracciones son equivalentes cuando equivalen a las mismas unidades.
Por ejemplo:
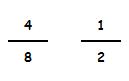
Estas dos fracciones son equivalente ya que equivalen a las mismas unidades:
4 : 8 = 0,5 unidades
1 : 2 = 0,5 unidades
¿Cómo sabemos cuando dos fracciones son equivalentes?
Para ello dividimos sus numeradores y sus denominadores, si guardan la misma proporción es que son equivalente:
Veamos un ejemplo:
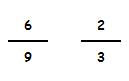
Dividimos sus numeradores: 6 : 2 = 3
Dividimos sus denominadores: 9 : 3 = 3
Guardan la misma proporción (3) luego estas dos fracciones son equivalentes.
Podemos comprobarlo.
La primera fracción equivale a 6 : 9 = 0,66 unidades
La segunda fracción equivale a 2 : 3 = 0,66 unidades
Veamos ahora un ejemplo de dos fracciones que no son equivalentes:
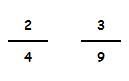
Dividimos sus numeradores: 2 : 3 = 0,66
Dividimos sus denominadores: 4 : 9 = 0,44
No guardan la misma proporción luego estas dos fracciones no son equivalentes.
Podemos comprobarlo.
La primera fracción equivale a 2 : 4 = 0,50 unidades
La segunda fracción equivale a 3 : 9 = 0,33 unidades
2.- Comparación de fracciones
¿Cómo puedo saber si una fracción es mayor o menor que otra?
Para ello vamos a distinguir:
Comparar fracciones con el mismo denominador
Comparar fracciones con distinto denominador
a) Comparar fracciones con el mismo denominador
Es mayor la fracción que tenga mayor el numerador.

Podemos comprobar que 2 / 4 = 0,5 mientras que 1 / 4 = 0,25, luego la primera fracción es mayor.
También podemos comprobar que 5 / 9 = 0,55 mientras que 3 / 9 = 0,33, luego la primera fracción es mayor.
b) Comparar fracciones con distinto denominador
En este caso puede ocurrir que tengan el mismo numerador o no.
b.1.- Si tienen el mismo numerador es mayor la que tenga menor denominador.

En este caso comprobamos que 8 / 3 = 2,66 mientras que 8 / 5 = 1,60, luego la primera fracción es mayor.
También podemos ver que 6 / 2 = 3,00 mientras que 6 / 4 = 1,50, luego la primera fracción es mayor.
b.2.- Si tienen distinto numerador entonces para poder comparalas hay que expresarlas con el mismo denominador:
Si los dos términos de una fracción se multiplican por el mismo número la fracción resultante es equivalente.
¿Y por qué número multiplicamos cada fracción? la primera fracción la multiplicamos por el denominador de la segunda, y la segunda por el denominador de la primera.
Veamos un ejemplo:
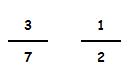
Para comparar estas dos fracciones, vamos a multiplicar los dos términos de la primera fracción por 2 (denominador de la segunda).
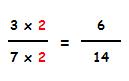
Podemos comprobar que al multiplicar numerador y denominador por el mismo número la fracción no cambia: 3 / 7 = 0,428 mientras que 6 / 14 = 0,428.
Y vamos a multiplicar los dos términos de la segunda fracción por 7 (denominador de la primera).
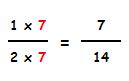
Ahora las dos fracciones ya tienen el mismo denominador, luego podemos compararlas:
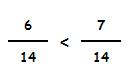
Vemos que la segunda fracción es mayor que la primera porque su numerador es mayor.

Ejercicios
1. Señala si los siguientes pares de fracciones son equivalentes (S) o no (N):
| 1) | 4/5 8/10 | |
| 2) | 3/5 9/5 | |
| 3) | 7/8 5/4 | |
| 4) | 2/3 5/6 | |
| 5) | 6/9 8/3 | |
| 6) | 1/4 2/5 | |
| 7) | 2/5 4/10 | |
| 8) | 1/3 3/9 | |
| 9) | 7/14 1/2 | |
| 10) | 1/6 2/12 | |
Corregir
Ver Solución
Limpiar | ||
2. De los siguientes pares de fracciones escribe en el recuadro en blanco la mayor:
| 1) | 4/7 5/7 | |
| 2) | 3/5 9/5 | |
| 3) | 7/8 5/8 | |
| 4) | 2/3 5/3 | |
| 5) | 6/9 8/9 | |
| 6) | 1/5 2/5 | |
| 7) | 3/7 6/7 | |
| 8) | 4/3 1/3 | |
| 9) | 9/4 6/4 | |
| 10) | 1/5 8/5 | |
Corregir
Ver Solución
Limpiar | ||
3. Representa con fracciones:
| 1) | Se divide un queso en 9 porciones y me tomo solo 2 | |
| 2) | De una colección de 70 cromos he conseguido reunir 45 | |
| 3) | He llenado de agua las tres cuartas partes de una piscina | |
| 4) | De los 11 jugadores de un equipo de fútbol se han lesionado 4 | |
| 5) | De 5 barras de pan que compré, 3 de ellas estaban duras | |
| 6) | De 10 preguntas del examen solo supe responder correctamente 3 | |
| 7) | De cada 10 votos 7 fueron para el partido independentista | |
| 8) | Un tercio de la población mundial vive en Asia | |
| 9) | De los 20 intentos que hice acerté en el blanco 14 veces | |
| 10) | Tengo en mi poder la mitad de la comida | |
Corregir
Ver Solución
Limpiar | ||


